6.5.1 二叉树的线索链表

　　对二叉树进行遍历的过程即为沿着某一条搜索路径对二叉树中的结点进行一次且仅仅一次访问，换句话说，就是按一定规则将一个处于层次结构中的结点排列成一个线性序列之后进行依次访问，这个线性序列或是先序序列、或是中序序列或是后序序列，在这些线性序列中每个结点（除第一个和最后一个外）有且仅有一个直接前驱和直接后继（在不致于混淆的情况下，我们省去直接二字）。例如右图所示二叉树中的数据元素"E" 在先序序列中的前驱是"D"，后继是"G"；而在中序序列中的前驱是"G"，后继是"H"；在后序序列中的前驱是"H"，后继是"B"。显然，这种信息是在遍历的动态过程中产生的，如果将这些信息在第一次遍历时就保存起来，则在以后再次需要对二叉树进行"遍历"时就可以将二叉树视作线性结构进行访问操作了。
　		  
　　
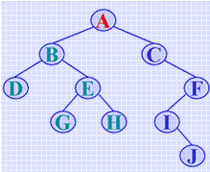
　　先序序列为： ABDEGHCFIJ
　　中序序列为： DBGEHACIJF
　　后序序列为： DGHEBJIFCA
　		  
  　　如何保存在遍历过程中得到的前驱和后继信息？最简单的办法是在结点中增加两个指针域分别指向该结点的前驱和后继，但如此做将使存储结构的存储密度大大降低。而另一方面，一个含 n 个结点的二叉链表中有 n+1 个链域的值为"NULL"，可以利用这些空的指针域存放指向前驱和后继的信息，由此得到的二叉树的存储结构称作"线索链表"，其中指向前驱或后继的指针称作"线索"。

　　线索链表的结构定义如下：

二叉树的二叉线索链表存储表示
　　typedef enum PointerType{ Link=0, Thread=1 };
　　　　　　　　　// 定义指针类型，以 Link 表示指针，Thread 表示线索
　　typedef struct BiThrNode{
　　　ElemType data;
　　　struct BiThrNode *Lchild, *Rchild; // 左右指针
　　　PointerType LTag, RTag;　　　　　　// 左右指针类型标志
　　} *BiThrTree;

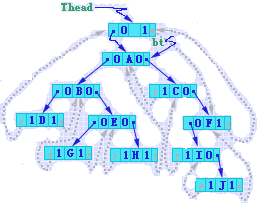
　　例如，右图二叉树的中序线索链表如下所示（图中所有实线表示指针，虚线表示线索）。
　
　　从图中可见，在线索链表中添加了一个"头结点"，头结点的左指针指向二叉树的根结点，其右线索指向中序序列中的最后一个结点，中序序列中的第一个结点的左线索和中序序列中的最后一个结点的右线索均指向头结点。这就好比将二叉树中所有结点置于一个双向循环链表之中，即可以从头结点出发，依照中序遍历的规则对二叉树中的结点依次进行"顺序"（和中序序列相同的次序）访问，或"逆序"（和中序序列相反的次序）访问。
   存储密度=
　　数据元素所占存储量/整个存储结构所占存储量

　
　
　
　
　
　
　
　　若结点的左指针类型标志为"Link"，则 Lchild 指向它的左子树根结点，否则指向它的"前驱"；
　　若结点的右指针类型标志为"Link"，则 Rchild 指向它的右子树根结点，否则指向它的"后继"。