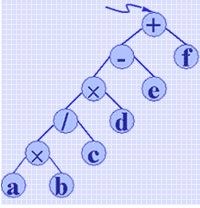
6.4.2 二叉树其它操作算法举例 　六、建表达式的二叉树 　　由此，按原表达式建二叉链表算法的基本思想为： 　　if (当前识别的字符 ch 是操作数) 　　　{ 建叶子结点; 暂存; } 　　else if (当前识别的字符ch是运算符) 　　　{ 　　　　和前一个运算符比较优先数; 　　　　若当前的优先数"高"，则暂存; 　　　　否则以前一运算符为根建立一棵新的子树(最近建立的 　　　　　　两棵子树分别为它的左右子树)并暂存; 　　　} 　　显然，在这个算法中需要两个栈，一个是运算符栈，其作用和表达式转换为后缀式的算法中相同，另一个是暂存"已经建好的子树根的指针"栈。		例一 　　　原表达式：a × b / c × d - e + f 　　　后 缀 式：a b × c / d × e - f + 　　由于'×'"领先"于'/'，则'×'和分别先建好的左右子树(操作数a和b)构成一个子树，又由于'/'"领先"于在它之后出现的'×'，则(a×b)就成为'/'的左子树，而由操作数 c 建成的叶子是它的右子树，依次类推，最后建成下列二叉树。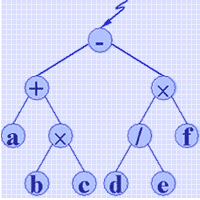 　　 例二 　　　原表达式：a + b × c - d / e × f 　　　后 缀 式：a b c × + d e / f × - 　　同理，由于'×'"领先"于'+'，则'×'和分别先建好的左右子树(操作数b和c)构成一个子树，又由于'+'"领先"于在它之后出现的'-'，则(a×b)就成为'+' 的右子树，而由操作数a建成的叶子是它的左子树，依次类推，最后建成下列二叉树。
	算法6.8 　　BiTree CrtExptree( char* exp ) 　{ 　　// 建立由合法的表达式字符串 exp 确定的只含二元运算符的 　　// 非空表达式树，返回其存储结构二叉链表的根结点指针 　　InitStack(S); Push(S,'#'); // S为暂存运算符的栈 　　InitStack(PTRS);　　　　　// PTRS为暂存子树根指针的栈 　　p=exp; ch=*p; 　　while(!(GetTop(S)=='#'&& ch=='#')) 　　{ 　　　if (!IN(ch,OP)) CrtNode( t, ch ); 　// 建叶子结点 　　　else { 　　　　switch (ch) { 　　　　　case'(': Push(S, ch); break; 　　　　　case')': { 　　　　　　Pop(S,c); 　　　　　　while (c!='(') 　　　　　　{ CrtSubtree(t,c); Pop(S,c);} // 建子树直至运算符的栈顶为'(' 　　　　　　break; 　　　　　} 　　　　　defult:{ 　　　　　　while (!GetTop(S,c) && (precede(c,ch))) 　　　　　　{ CrtSubtree(t,c); Pop(S,c);} 　　　　　　　　　　　　　　　　// 建子树直至运算符栈顶运算符的优先数低 　　　　　　if ( ch !='#') Push( S,ch); 　　　　　　break; 　　　　　} // defult 　　　　} // switch 　　　} // else 　　　if (ch !='#') { p++; ch = *p; } 　　} // while 　　Pop(S, c); Pop( PTRS, t ); 　　DestroyStack(S); DestroyStack(PTRS); 　　return t; 　} // CrtExptree 　　算法的执行过程如动画所示。		OP为运算符和括弧的集合，IN(ch,OP) 为 "FALSE" 时表示 ch 为操作数。 其中建叶子结点的算法为： 　void CrtNode(BiTree& T,char ch) { 　if (!(T= new BiTNode)) 　　exit(OVERFLOW); 　T->data = char; 　T->Lchild = T->Rchild = NULL; 　Push(PTR,T); } 建子树的算法为： 　void CrtSubtree (Bitree& T,char c) { 　if (!(T= new BiTNode)) 　　exit(OVERFLOW); 　T->data = c; 　Pop(PTR, rc); T->Rchild = rc; 　Pop(PTR, lc); T->Lchild = lc; 　Push(PTR, T);}