六、建表达式的二叉树
一个含二元运算符的表达式由一个运算符和两个操作数组成，而操作数本身也可以是表达式。因此表达式的定义也是递归的。称在运算符左边出现的操作数为第一操作数，称在运算符右边出现的操作数为第二操作数，这样的表达式可以一个"正则二叉树"表示，以左子树表示第一操作数，以右子树表示第二操作数，根结点的数据元素为运算符。如下列表达式
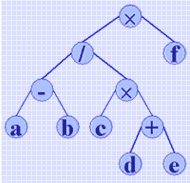
(a-b)/(c×(d+e))×f
可以用右图的二叉树表示。对此二叉树进行先序、中序和后序遍历分别得到二叉树的先序序列"×/-ab×c+def"（即表达式的前缀表示）、二叉树的中序序列"a-b/c×d+e×f"（即表达式的中缀表示）和二叉树的后序序列"ab-cde+×/f×"（即表达式的后缀表示）。
那么如何建立这个表达式的存储结构二叉链表？
假设不考虑空的表达式且以单字母表示操作数，若以"前缀表示"的格式输入表达式，则建立二叉链表的算法和算法6.6极为相似。算法的基本思想为：
若输入的字符是"字母字符"，则建立叶子结点；
否则
建立根结点；
递归建立左子树(第一操作数表达式)；
递归建立右子树(第二操作数表达式)；
假设以上述的"后缀表示"格式输入，则建树的过程和3.2.5节中讨论的"后缀式求值"的过程类似。但无论是前缀式还是后缀式都是从原表达式转换得到，因此实际应用中还是希望能从原表达式直接建立二叉树(即它的存储结构二叉链表)。
"正则二叉树"是指树中没有度为1的结点的二叉树。
|
|||
|
你已经会写对后缀式求值的算法，那么如何改为建二叉树的算法？
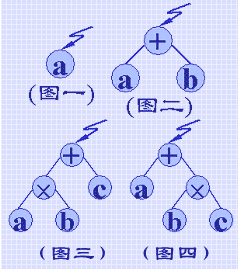
1) 只含一个操作数 a 的表达式，对应的二叉树中只含一个叶子结点(图一)。
2) 只含一个运算符的表达式 a+b，对应的二叉树的形态是"其左右子树均为叶子结点"(图二)。由于表达式中只有一个运算符，显然它是根，其左右子树分别为它的第一操作数和第二操作数。
3)当表达式中的运算符多于一个时，显然存在一个"哪一个是根结点"的问题。例如，表达式 a×b+c 的二叉树如图三所示，表达式 a+b×c 的二叉树如图四所示。它们的差别是显然的，在前一个表达式中，因为后面的运算符的优先数"低于"前面的运算符的优先数，则b是在它之前的运算符的第二操作数，a×b 是+的第一操作数。而在后一个表达式中，由于后面的运算符的优先数"高于"前面的运算符的优先数，则b是在它之后的运算符的第一操作数，b×c 是+的第二操作数。
由此可见，从原表达式构造二叉树的过程类似于将原表达式转换成后缀式的过程，"构建一棵以运算符为根的二叉树"相当于进行运算，因此对原表达式中出现的每一个运算符是否即刻构建一棵以它为根的子树（即是否即刻进行运算）取决于在它后面出现的运算符，如果它的优先数"高或等于"后面的运算，则它的运算先进行，即和已经建好的左右子树构成一棵以它为根的二叉树，否则就得等待在它的右子树建成（即在它之后出现的所有优先数高于它的"运算"都完成）之后再建以它为根的二叉树。
可以对照3.2.5中举的两个表达式的例子来看建树的过程。