四、建立二叉树的存储结构--二叉链表
在输入数据正确的前提下，由此建立二叉链表的算法为：
若输入的字符是'#'，则建立空树；
否则
建立根结点；
递归建立左子树的二叉链表；
递归建立右子树的二叉链表。
算法 6.6 void CreateBiTree(BiTree &T)
{
// 在先序遍历二叉树的过程中输入二叉树的"先序字符串"，
// 建立根指针为 T的二叉链表存储结构。在先序字符串中，
// 字符'#'表示空树，其它字母字符为结点的数据元素
cin >> ch ；
if (ch=='#') T=NULL; // 建空树
else {
T = new BiTNode ; // "访问"操作为生成根结点
T->data = ch;
CreateBiTree(T->Lchild); // 递归建(遍历)左子树
CreateBiTree(T->Rchild); // 递归建(遍历)右子树
} // else
} // CreateBiTree
对二叉树的不同定义可得不同的建二叉链表的算法。为简化问题，设二叉树中结点的元素均为一个单字符，并以"#"表示空树。假设二叉树以由"根"、"左子树串"和"右子树串" 联接而成的字符串表示，则建立二叉链表的算法应该是一个"先序遍历"的过程，并且遍历过程中"访问"的操作应是"识别输入的字符并作相应操作"。
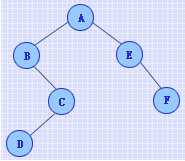
例如，空树以"#"表示，只有一个根结点A的二叉树以"A##"表示，下列二叉树则以"AB#CD###E#F##"表示。
以此二叉树为例算法6.6的执行过程如动画所示。