从二叉树的结构定义得知,二叉树是由"根结点"、"左子树"和"右子树"三部分构成,则遍历二叉树的操作可分解为"访问根结点"、"遍历左子树"和"遍历右子树"三个子操作,并且由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样"递归"进行。因此整个遍历的操作只要在一条搜索路径上一次完成这三个子操作即可。
右图所示为对二叉树进行遍历的先左后右的搜索路径。从图可得知两个结论:1) 由于左右子树互不相交,因此对左子树的遍历一定不会访问到右子树上的结点,反之对右子树的遍历也一定不会访问到左子树,因此沿这条搜索路径必可实现对二叉树中每个结点都访问到且只访问一次;2)也正由于左右子树不相交,因此在遍历了左子树之后必须回到根结点才能继续遍历右子树。由此可见,在这条搜索路径上从进入二叉树到离开二叉树,一共三次遇到根结点,因此访问根结点的操作可在任意一次也只能在其中一次进行。由此得到以下三个遍历二叉树的算法:
|
先序遍历二叉树
|
中序遍历二叉树
|
后序遍历二叉树
|
| 若二叉树为空,则空操作; 否则 (1) 访问根结点; (2) 先序遍历左子树; (3) 先序遍历右子树。 |
若二叉树为空,则空操作; 否则 (1) 中序遍历左子树; (2) 访问根结点; (3) 中序遍历右子树。 |
若二叉树为空,则空操作; 否则 (1) 后序遍历左子树; (2) 后序遍历右子树; (3) 访问根结点。 |
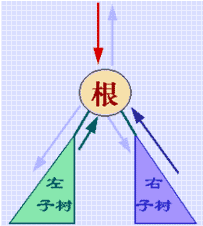
第一次走到根结点即"访问"为"先序遍历",从左子树回来再"访问"为"中序遍历",从右子树回来再 "访问"为"后序遍历"。如动画所示。
由以上遍历算法的定义很容易写出对应的递归算法。
void Preorder (BiTree T,void(*visit)( BiTree ))
{
// 先序遍历以T为根指针的二叉树
if (T) { // T=NULL时,二叉树为空树,不做任何操作
visit(T); // 通过函数指针 *visit 访问根结点
Preorder(T->Lchild, visit); // 先序遍历左子树
Preorder(T->Rchild, visit); // 先序遍历右子树
} // if
}