6.3.2 链式存储结构

　三、双亲链表

算法 二叉树的双亲链表存储表示
　　const MAXSIZE = 100;　　　　　　　　// 暂定二叉树中结点数的最大值为100
　　typedef struct BPTNode {　　　　　　　　// 结点结构
　　　ElemType data;
　　　int *parent;　　　　　　　　　　　　　 // 指向双亲的指针
　　　char LRTag;　　　　　　　　　　　　　　　// 左、右孩子标志域
　　} BPTNode
　　typedef struct BPTree{　　　　　　　　　// 树结构
　　　BPTNode *nodes; 　　　　　　　　　　　　// 初始化时分配存储空间
　　　int nodeNum; 　　　　　　　　　　　　　// 结点数目
　　　int root;　　　　　　　　　　　　　　　// 根结点的位置
　　} BPTree
　　　cin>>BT.nodeNum;　　　　　　　　　　　 // 输入结点数目
　　　BT.root=0;
　　　cin>> BT.nodes[0].data; 　　　　　　　　// 输入根
　　　BT.nodes[0].parent = -1;　　　　　　　　// 根的双亲为空
　　　BT.nodes[0].LRTag = 'L';
　　　for (i=1; i<BT.nodeNum; i++)
　　　{
　　　　cin>> BT.nodes[i].data >> F >>BT.nodes[i].LRtag;
　　　　k=i-1;
　　　　while (k>=0 && BT.nodes[k].data != F) k--; // 查询双亲
　　　　if (k<0) return FALSE; 　　　　　　　// 没有找到双亲
　　　　BT.nodes[i].parent = k;
　　　　return TRUE;
　　　}
　　}
  
　　显然，也可以只含双亲信息的链表表示二叉树，但由于二叉树的子树有左、右之分，因此在只含双亲指针的结点中还必须包含一个"左右标志"的信息。

　　双亲链表的结点结构：

data
parent
LRTag

　　显然由这种结构的结点构成的链表无法只用一个指针来表示，所有的结点必须存放在一个地址连续的存储空间中，即在构造存储结构时首先需为结点动态分配存储空间。结点在数组中的存储位置由输入的先后次序自然形成。

　　

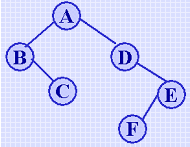
　　例如上图所示二叉树的输入数据为：
　6,A,(B,A,L),(C,B,R),(D,A,R),(E,D,R),(F,E,L)

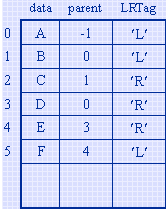
　　则按算法6.1建立的双亲链表如下所示。