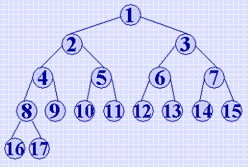
6.2.2 二叉树的几个特性 　四、具有n个结点的完全二叉树的深度为 log2n+1。 　　假设该完全二叉树的深度为 k，则根据特性二和完全二叉树的定义 　　　2k-1 -1 <n ≤ 2k -1 或 2>k-1 ≤ n < 2k 　　对后者取对数便得 k-1 ≤ log2n < k 　　因为k是整数，所以 k=[log2n]+1 。		不等式 k-1 ≤ log2n < k 　表明： 　　若 log2n 是整数，则等于 k-1， 　　若 log2n 不是整数，则它大于 k-1 而小于 k。 　　log2n 表示仅取 log2n 的整数部分，舍去它的小数部分。
	五、如果对一棵有 n 个结点的完全二叉树（其深度为 log2n+1）的结点按层序（从第1层到第 log2n+1 层，每层从左到右）从1起开始编号，则对任一编号为 i 的结点(1≤i≤n)，有 　(1) 如果 i=1，则编号为 i 的结点是二叉树的根，无双亲；如果 i>1，则其双亲结点 parent(i) 的编号是 i/2。 　(2) 如果 2i>n，则编号为 i 的结点无左孩子（编号为 i 的结点为叶子结点）；否则其左孩子结点 lChild(i) 的编号是 2i 。 　(3) 如果 2i+1>n，则编号为 i 的结点无右孩子；否则其右孩子结点 rChild(i) 的编号是结点 2i+1。 　　在此省略这个性质的证明，读者可以从图直观验证这个结果。