二叉树的抽象数据类型定义如下：
ADT BinaryTree {
数据对象：D 是具有相同特性的数据元素的集合。
数据关系：
若 D 为空集，称 BinaryTree 为空二叉树；
否则 关系 R={H}：
(1) 在 D 中存在唯一的称为根的数据元素 root，它在关系 H 下无前驱；
(2) D 中其余元素必可分为两个互不相交的子集 L 和 R，每一个子集都是一棵符合本定义的二叉树，并分别为 root 的左子树和右子树。如果左子树 L 不空，则必存在一个根结点
，它是
root 的"左后继"(<root,>∈H)，如果右子树
R 不空，则必存在一个根结点 
为 root 的"右后继"(<root,>∈H)。
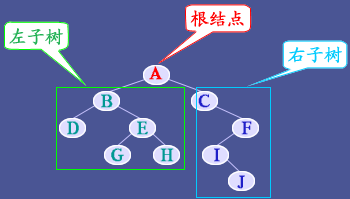
如图示为含10个元素的二叉树，其中 A为"根"，无前驱。其余9个元素分为两个互不相交的子集 L={B,D,E,G,H}，R={C,F,I,J}，分别为 A 的左子树和右子树。其中，B 为左子树的根，它是 A 的左后继；C 为右子树的根，它是 A 的右后继。在右子树R 中，C 为根，其余元素分为两个子集 {} 和 {F,I,J} 分别构成 C 的左子树和右子树，即 C 的左子树为空树，C 的右子树中，F 为根结点，它是 C 的右后继，同时，{I,J} 为 F 的左子树，其中 I 为 F 的左后继，而 F 的右子树为空树。继续分解可得，I 的左子树为空树，右子树 {J} 中的根 J 为 I 的右后继，它的左右子树都为空树。
二叉树和树是两种不同的树型结构，二叉树不等同于度为2的有序树。
|
|||
|
为什么？你能举出一个例子来吗？