树型结构是一类重要的非线性结构，正如在课前思考题所看到的，树型结构广泛用于描述家族谱系以及其它社会组织结构。在计算机领域中，如编译程序中的语法结构和数据库中的信息组织也都需要借用树来描述。本章将讨论树和二叉树两种树型结构。
　		      
  　 树的抽象数据类型的定义如下：

ADT Tree {
　数据对象：D是具有相同特性的数据元素的集合。

　数据关系：
　　若 D 为空集，则称为空树；
　　若 D 中仅含一个数据元素，则关系R为空集；
　　否则 R={H}，
　　 (1) 在D中存在唯一的称为根的数据元素 root，它在关系H下无前驱；
　　 (2) 当n>1时，其余数据元素可分为 m(m>0) 个互不相交的(非空)有限集 T1,T2,…,Tm, 其中每一个子集本身又是一棵符合本定义的树，称为根 root 的子树，每一棵子树的根 xi 都是根 root 的后继，即 <root,xi> H,i=1,2,…,m。

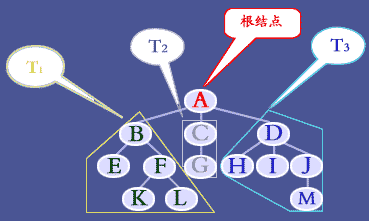
　　　		   　　例如所示图为含13个数据元素的集合，其中，A 为"根"，其余12个数据元素分为3个互不相交的子集 T1={B,E,F,K,L}、T2={C,G}和T3={D,H,I,J,M}，每个子集都是一棵树，称为A的子树，它们的根结点都是 A的后继。这是一个递归的定义，如在子树T1中，B是根，其余元素分为2个互不相交的子集T11={E}和 T12={F,K,L}，每个子集构成一棵B的子树，子树中的根结点是B的后继，依次类推。换句话说，在这13 个数据元素之间存在下列关系：
R={<A,B>,<A,C>,<A,D>,<B,E>,<B,F>,<C,G>,
　<D,H>,<D,I>,<D,J>,<F,K>,<F,L>,<J,M>}。

　　可见，这是一棵"有向树"，虽然图上的线条没有标上箭头，但实际上存在着有向关系。因此，树是一种层次分明的结构，约定根的层次为1，其余元素层次的定义为：若根的层次为，则子树根的层次为+1。
　　然而，子树之间可能存在两种情况，如果子树之间映射客观存在的次序关系，则为"有序树"，否则为 "无序树"。
　　称根和子树根之间的连线为"分支"，则数据元素和所有指向子树根的分支构成树中一个"结点"，其分支的个数定义为"结点的度"，如结点B的度为2，D 的度为3。树中所有结点度的最大值定义为"树的度"。称度为零的结点为"叶子"或"终端结点"，如结点 K,L,G 等，反之所有度不为零的结点被称作"分支结点" ，如结点 F,J 等。