三、十字链表
稀疏矩阵的十字链表存储表示typedef struct OLNode { // 结点结构定义
int i, j; // 该非零元的行和列下标
ElemType e;
struct OLNode *right, *down; // 该非零元所在行表和列表的后继链域
} *OLink;
typedef struct { // 链表结构定义
OLink *rhead, *chead; // 行和列链表头指针向量基址由CreateSMatrix分配
int rows, cols, terms; // 稀疏矩阵的行数、列数和非零元个数
} CrossList;
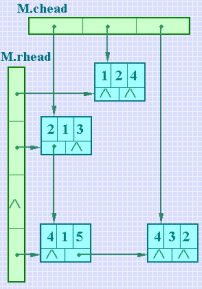
从上述结构定义可见，每个非零元以含5个域的结点表示，除了表示非零元信息的三元组(i,j,e)之外，添加了两个链域：一个是链接同一行下一个非零元结点的 right 域，另一个是链接同一列下一个非零元结点的 down 域。每个非零元既是某个行链表中的一个结点，又是某个列链表中的一个结点，整个矩阵构成了一个十字交叉的链表，故称为十字链表，以两个分别存放行链表的头指针和列链表的头指针的一维数组表示之。
例如矩阵
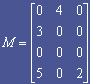的十字链表如图所示。
|
|||
|
你有没有发现以上讨论的矩阵运算有没有一个"适于采用顺序结构"的共同特点？
反之，如果矩阵运算的结果将增加或减少已知矩阵中的非零元的个数，则显然不宜采用顺序存储结构，而应以链式映象作为三元组线性表的存储结构。本小节讨论的十字链表即为稀疏矩阵的一种链式映象。
算法 5.4bool CreateSMatrix_OL (CrossList &M)
{
// 创建稀疏矩阵M的十字链表存储结构,若存储分配失败，则返回FALSE
cin >> M.rows >> M.cols >> M.terms;// 输入M的行数、列数和非零元个数
if (!(M.rhead = new OLink[M.rows+1]))
return FALSE; // 存储分配失败
if (!(M.chead = new OLink[M.cols+1]))
return FALSE; // 存储分配失败
M.rhead[] = M.chead[] = NULL ;
// 初始化行列头指针向量；各行列链表为空链表
for (scanf(&r, &c, &v); i!=0; scanf(&r, &c, &v))
{ // 按任意次序输入非零元
if (!(p = new OLNode)) return FALSE;
p->i = r; p->j = c; p->e = v; // 生成结点
if (!M.rhead[r] || c < M.rhead[r]->j) {
p->right = M.rhead[r]; M.rhead[r] = p;
}
else { // 寻查在行表中的插入位置
for( t = M.rhead[r];!t->right && t->right->j < c; t=t->right; );
p->right = t->right; t ->right = p;
} // 完成行插入
if (!M.chead[c] || r < M.chead[c]->i) {
p->down = M.chead[c]; M.chead[c] = p;
}
else { // 寻查在列表中的插入位置
for( q = M.chead[c];!q->down && q->down->i < r; q = q->down; );
p->down = q->down; q->down = p;
} // 完成列插入
} // for
return TRUE;
} // CreateSMatrix_OL
对于每个输入的非零元，既要插入在行链表中，又要插入在列链表中，算法5.4没有限定输入顺序，因此对每个输入的非零元都需要在相应的行链表和列链表中查询结点的插入位置，因此算法5.3的时间复杂度为O (t×s)，其中 t 为所建矩阵中非零元的个数，s 为其行列的最大值。
显然这种存储表示便于进行将改变其中非零元状态的矩阵运算，如将一个矩阵加到另一个矩阵上的运算等。