二、行逻辑链接的顺序表
现在讨论当以行逻辑链接顺序表表示时,如何进行两个矩阵相乘的运算。
当以二维数组表示矩阵时的矩阵相乘的乘法想必大家已经很熟悉了。
void multiplication(double M[m][n],
double N[n][p], double Q[m][p])
{
for (i=0; i<m; i++)
for (j=0; j<p; j++)
{
Q[i][j]=0;
for (k=0; k<n; k++)
Q[i][j]+=M[i][k]*N[k][j];
}
}
从上述算法可见,乘积矩阵中的每个元是由 M 矩阵中的一行和 N 矩阵中一列的对应元的乘积和。如果 M[i][k] 和 N[k][j] 两者中有一个为零元,其乘积即为零。由此可得如下三个结论:1)乘积矩阵Q的非零元仅由M和N中的非零元相乘得到,换句话说,为求得两个稀疏矩阵相乘的乘积,只需要对 M 和 N 中的非零元进行运算即可;2)从矩阵相乘的规则得知,并非两者中每个元素都要进行彼此相乘,对 M 中的每个非零元,只要在 N 中查找其行号等于它的列号的非零元相乘即可;3)在上述算法中,Q 的每个元素是由 M 中的一行和N中的一列相应元素连续相乘相加得到的,但在行逻辑链接的三元组顺序表中要连续找到同一列的元素是很不方便的,因此需要改变计算的顺序,寻找新的算法。
对行逻辑链接的三元组顺序表表示的稀疏矩阵,我们不易直接求得 Q 的一个非零元,但可以设法求得 Q 的"一行"非零元。因为 Q 的一行非零元一定是由 M 的相应行的非零元得到的,并且对Q的每个元以"累加"的方式求得。具体作法为:
设累加器 ctemp 的容量为 p( p 为 Q 中列数,即 N 的列数)
初始化累加器 ctemp[ ]=0;
for (M 中第 i 行的所有非零元 M.data[p])
{
brow=M.data[p].j; // 该非零元在 M 中的列号
for (N中第 brow 行的非零元 N.data[q])
{
ccol= N.data[q].j; // 该非零元在N中的列号
ctemp[ccol-1]+=M.data[p].e * N.data[q].e;
}
}
容易看出上述运算的结果 ctemp 中所有非零分量即为 Q 中第 i 行的所有非零元。实际上,乘积 Q 中哪些元为零哪些元为非零,并非从 M 和 N 的情况一下子就能看出来的,也只有通过上述运算的结果才能得到 Q 中一行的非零元,之后可按其列号大小依次存入 Q.data 中。
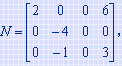
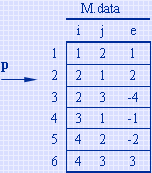
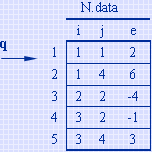
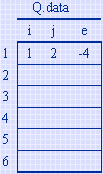
例如:对所举例子中的矩阵,当 i=2 时,M 在 data 中的第一个非零元的位置 p=2,则 brow=1,矩阵 N 中有两个非零元,q=1 和2。当 q=1 时,因为 N.data[q].j 为1,则M.data[p].e*N.data[q].e应叠加到 ctemp[0] 中去,因为它是构成 Q[2][1] 的部分积。同理,当 q=2 时,因为N.data[q].j为4,则 M.data[p].e*N.data[q].e 应叠加到 ctemp[3] 中去,因为它是构成 Q[2][4] 的部分积。对 M 中第2行的另一个非零元,即 p=3,此时 brow=M.data[p].j=3,q=4和5,作如上相同处理之后,ctemp 中各分量的值依次为4,4,0,0。由此得到 Q 中第2行的两个非零元,可依次将它们放入 Q.data 中。
上述 p 和 q 的值均可从 M 和 N 的行逻辑信息 rpos 中得到。
例如:
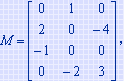
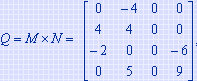
ctemp
|
0
|
1
|
2
|
3
|
||||
|
|||||||
M.rpos的值为:
|
行号
|
1
|
2
|
3
|
4
|
(5)
|
||||||
| M.rpos |
|
||||||||||
N.rpos的值为:
|
行号
|
1
|
2
|
3
|
(4)
|
||||||
| M.rpos |
|
|||||||||