一、三元组顺序表
当以三元组顺序表表示稀疏矩阵时,是否仍然便于进行运算呢?在此以"转置"运算为例讨论算法。
假设前面所列举的矩阵M的转置矩阵为 T,则按照矩阵转置的定义,

对比M和T,T的行数、列数和非零元的个数等于M的列数、行数和非零元的个数,且T中的每个非零元和M中的非零元相比,它们的值相同,但行列号互换。由于三元组表中元素的顺序约定为以行序为主序,即在 T 中非零元的排列次序是以它们在 M 中的列号为主序的。因此转置的主要操作就是要确定M中的每个非零元在T的三元组顺序表中的位序,即分析两个矩阵中值相同的非零元分别在 M.data 和 T.data 中的位序之间的关系是什么。
例如:M.data 中第2个元素(1,5,-7)转置到T中的位序为4,为什么?因为该元在M中的列号为5,行号为1,又 M 中前4列中非零元的总数为3。换句话说,T 中前4行中只有3个非零元,而值为-7的非零元是 T 中第5行的第一个非零元,当然在 T.data 中应该位居第4。
由此,转置算法的操作步骤为:
1.求 M 矩阵的每一列中非零元的个数;
2.确定T的每一行中第一个非零元在 T.data 中的序号;
3.将 M.data 中每个元素依次复制到 T.data 中相应位置。
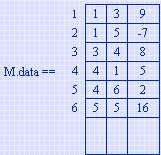
M的三元组顺序表为:
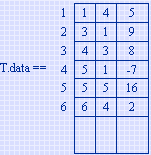
T 的三元组顺序表为:
以下表格中的三行依次为:M 的列号、M 中各列非零元的总数和 T 中每一行第一个非零元在 T.data 中的序号:
|
col
|
1
|
2
|
3
|
4
|
5
|
6
|
|
num[col]
|
1
|
0
|
1
|
1
|
2
|
1
|
|
rpos[col]
|
1
|
2
|
2
|
3
|
4
|
6
|
表格中的 col 指示 M 中的列号,即 T 中的行号,则 rpos 中的值可递推求得:
rpos[1] = 1;
rpos[col] = rpos[col-1]+num[col-1]
第一行的第一个非零元在 data 中的位置肯定是1,而之后其它各行的第一个非零元在 data 中的位置显然取决于它的前一行中的非零元的个数。