5.2.2 稀疏矩阵的压缩存储方法 　　如果矩阵中只有少量的非零值元，并且这些非零值元在矩阵中的分布没有一定规律，则称为随机稀疏矩阵，简称为稀疏矩阵。至于矩阵中究竟含多少个零值元才被称为是稀疏矩阵，目前还没有一个确切的定义，它只是一个凭人的直觉来了解的概念。假设在 mn 的矩阵中有 t 个非零值元，令 ，称为矩阵的稀疏因子，则通常认定≤0.05的矩阵为稀疏矩阵。
	如何存储稀疏矩阵中的非零值元？ 　　首先应该分析一下，如果仍然采用二维数组表示稀疏矩阵，那么它的弊病是什么？ 　　一、浪费空间，二、浪费时间。 　　前者是指存放了大量没有用的零值元素，后者是指在进行矩阵的运算中进行了很多与零元素的运算。 　　由此解决稀疏矩阵压缩存储的目标是：1)尽可能减少或不存储零值元；2)尽可能不作和零值元进行的运算；3)便于进行矩阵运算，即易于从一对行列号找到矩阵的元，易于找到同一行或同一列的非零值元。 　　由于压缩存储的基本宗旨是只存放矩阵中的非零值元，则在存储非零元的值的同时必须记下它在矩阵中的位置，反之，一个三元组 唯一确定了矩阵A中的一个非零值元,由此可以"其数据元素为上述三元组的线性表"表示稀疏矩阵，并且非零元在三元组线性表中是"以行为主"有序排列的。相应于线性表的两种存储结构可得到稀疏矩阵的不同压缩存储方法。		对稀疏矩阵进行压缩存储时不存或少存零值元是自然的，由于存储不是最后目的，重要的尚需对矩阵进行运算，因此在进行压缩存储时必须考虑到运算的方便。首先必须容易从找到矩阵的元(包括零值元)，其次，很多矩阵运算是按行或按列进行的，因此需要方便地找到同一行或同一列中紧接着出现的 "下一个" 非零值元。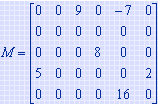 　例如表示矩阵 　　　 的三元组线性表为： 　((1,3,9),(1,5,-7),(3,4,8),(4,1,5), 　　　　　　　　　　　　　　(4,6,2),(5,2,16))