矩阵是数值程序设计中经常用到的数学模型，它是由 m 行和 n 列的数值构成（m=n 时称为方阵）。在用高级语言编制的程序中，通常用二维数组表示矩阵，它使矩阵中的每个元素都可在二维数组中找到相对应的存储位置。然而在数值分析的计算中经常出现一些有下列特性的高阶矩阵，即矩阵中有很多值相同的元或零值元，为了节省存储空间，需要对它们进行"压缩存储"，即不存或少存这些值相同的元或零值元。
5.2.1 特殊矩阵的压缩存储方法
如果矩阵中值相同的元素或零元素在矩阵中的分布有一定规律，则称之谓"特殊矩阵" 。大致有这样三类特殊矩阵：
1. 对称矩阵：若 n 阶方阵A中的元满足特性
= 
1≤i,j≤n则称为 n 阶对称矩阵；
2. 三角矩阵：若 n 阶方阵中下(上)三角(不包括对角线)中的元均为常量 c 或 0，则称为上(下)三角矩阵；
3. 对角矩阵：若n阶方阵中的非零值元都集中在以主对角线为中心的(由k条对角线组成的)带状区域中，则称为k对角矩阵。
若为对称矩阵中的每一对值相同的元素分配一个存储空间，则可将矩阵中 n2 个元压缩存储到 n(n+1)/2 个存储空间中。
假设以一维数组 sa[n(n+1)/2] 压缩存储n阶对称方阵A，则一维数组中的数据元素和方阵中的元
之间存在着下列一一对应的关系：
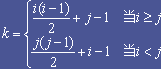
对于任意给定一对行列号(i,j)，均可在 sa 中找到方阵的元 ，反之，对于所有的
k=0,1,…,n(n+1)/2-1，都能确定sa[k] 中的元素在矩阵中的位置(i,j)。
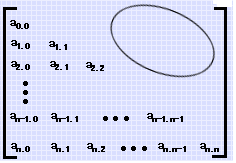
三角矩阵示例
对角矩阵示例
由于特殊矩阵中的非零值元素在矩阵中的分布有着一定的规律，则可将这些非零值元连续存储在一个一维数组中。即矩阵中的任何一个元和它们在一维数组中的位置之间存在着某种"转换关系"，并且这种转换关系可以用数学公式表示之。
显然，对于下(上)三角矩阵和对角矩阵也可得到类似对应关系。