【基础知识题】
1. 假设有二维数组 A6×8,每个元素用相邻的 6 个字节存储,存储器按字节编址。已知 A 的起始存储位置(基地址)为 1000,计算:
(1) 数组 A 的体积(即存储量);
(2) 数组 A 的最后一个元素 a57 的第一个字节的地址;
(3) 按行存储时,元素 a14 的第一个字节的地址;
(4) 按列存储时,元素 a47 的第一个字节的地址。
2. 假设按低下标优先存储整数数组A9×3×5×8时,第一个元素的字节地址是 100,每个整数占四个字节。问下列元素的存储地址是什么?
(1) a0000 (2) a1111 (3) a3125 (4) a8247
3. 按高下标优先存储方式(以最右的下标为主序),顺序列出数组 A2×2×3×3 中所有元素 aijkl,为了简化表达,可以只列出 (i,j,k,l) 的序列。
4. 将下面的式子改写为一个等式的形式。
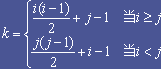
5. 设有上三角矩阵(aij)n×n,将其上三角元素逐行存于数组 B[m] 中( m 充分大) ,使得 B[k]=aij 且 k=f1(i)+f2(j)+c。试推导出函数 f1,f2 和常数 c (要求 f1 和 f2 中不含常数项)。
6. 设有三对角矩阵(aij)n×n,将其三条对角线上的元素存于数组 B[3][n] 中,使得元素 B[u][v]=aij,试推导出从(i,j) 到(u,v) 的下标变换公式。
7. 设有三对角矩阵(aij)n×n,将其三条对角线上的元素逐行地存于数组
B[3n-2] 中,使得 B[k]=aij,求:
(1) 用 i,j 表示 k 的下标变换公式;
(2) 用 k
表示 i,j 的下标变换公式。
8. 假设一个准对角矩阵

按以下方式存于一维数组 B[4m] 中
写出由一对下标 (i,j) 求 k 的转换公式。
【基础知识题】