一、顺序栈类型的定义
void InitStack (Stack &S,int maxsize)
{
// 构造一个最大存储容量为 maxsize 的空栈 S
if (maxsize == 0)
maxsize = MAXLISTSIZE;
S.base = new SElemType[maxsize];
if (!S.base) exit(1); // 存储分配失败
S.stacksize = maxsize;
S.top = 0; // 空栈中元素个数为0
}
在此只给出其中4个函数的定义。
对顺序栈来说,空栈的初始化和顺序表的初始化完全相同。这不奇怪,因为它们的结构是一样的。也就是说,并非对栈而言取不到除栈顶之外的元素,而是对栈类型来说,不允许这种操作。
在此定义中,栈顶指针的值恰为当前栈中元素个数,栈顶指针的初值为0和栈中元素个数为0是同一个含义。
bool GetTop (Stack S, ElemType &e)
{
// 若栈不空,则用 e 返回S的栈顶元素,并返回TRUE;否则返回FALSE
if (S.top == 0) return FALSE;
e = *(S.base + S.top-1); // 返回非空栈中栈顶元素
return TRUE;
}
*(S.base + S.top-1)是S.base[S.top-1] 的另一种写法,其实质相同。
bool Push (Stack &S, ElemType e)
{
// 若栈的存储空间不满,则插入元素 e 为新的栈顶元素,
// 并返回 TRUE;否则返回 FALSE
if (S.top == S.stacksize) // 栈已满,无法进行插入
return FALSE;
*(S.base + S.top) = e; // 插入新的元素
++S.top; // 栈顶指针后移
return TRUE;
}
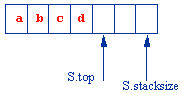
图中的顺序栈的最大容量为7,当前栈中元素个数为4,因此,我们也可认为栈顶指针总是指在栈顶元素的后面一个位置上。
bool Pop (Stack &S, ElemType &e)
{
// 若栈不空,则删除S的栈顶元素,用 e 返回其值,
// 并返回 TRUE;否则返回 FALSE
if (S.top == 0) return FALSE;
e = *(S.base + S.top-1); // 返回非空栈中栈顶元素
--S.top; // 栈顶指针前移
return TRUE;
}
和 GetTop 不同仅在于多一句移动指针的语句。
显然,顺序栈的基本操作的时间复杂度,除"遍历"之外,均为常量级的,即O (1)。