栈（Stack）是限定只能在表的一端进行插入和删除操作的线性表。在表中，允许插入和删除的一端称作"栈顶(top)"，不允许插入和删除的另一端称作"栈底(bottom)" 。
其类型定义如下：
ADT Stack {
数据对象：D＝{
| ∈ElemSet,
i=1,2,...,n, n≥0 }数据关系：R1＝{ <
,
>| ,
∈D,
i=2,...,n }约定
端为栈顶，
端为栈底。基本操作：
InitStack(&S)
操作结果：构造一个空栈 S。
DestroyStack(&S)
初始条件：栈 S 已存在。
操作结果：栈 S 被销毁。
ClearStack(&S)
初始条件：栈 S 已存在。
操作结果：将 S 清为空栈。
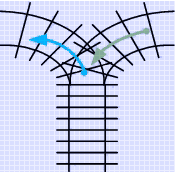
通常称往栈顶插入元素的操作为"入栈"，称删除栈顶元素的操作为"出栈"。因为后入栈的元素先于先入栈的元素出栈，故被称为是一种"后进先出"的结构，因此又称LIFO（LastIn First Out的缩写）表。很多书上都以如下图所示的铁路调度站形象地表示栈的这个特点。
初始条件：栈 S 已存在。
操作结果：若栈 S 为空栈，则返回TRUE，否则返回FALSE。
StackLength(S)
初始条件：栈 S 已存在。
操作结果：返回栈 S 中元素个数，即栈的长度。
初始条件：栈 S 已存在且非空。
操作结果：用 e 返回S的栈顶元素。
Push(&S, e)
初始条件：栈 S 已存在。
操作结果：插入元素 e 为新的栈顶元素。
这是入栈操作，在当前的栈顶元素之后插入新的栈顶元素。
初始条件：栈 S 已存在且非空。
操作结果：删除 S 的栈顶元素，并用 e 返回其值。
StackTraverse(S, visit( ))
初始条件：栈 S 已存在且非空，visit( )为元素的访问函数。
操作结果：从栈底到栈顶依次对S的每个元素调用函数visit( )，
一旦visit( )失败，则操作失败。
} ADT Stack
这是对栈进行从栈底到栈顶的"遍历"操作，应用较多的场合是，输出栈中所有数据元素。
栈的基本操作集和线性表相比要小的多，但它们在应用程序中都能用到。