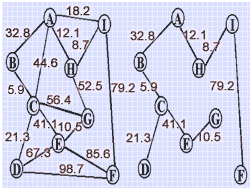
瑞士的计算机专家在1976年出版了一本书，书名为《算法+数据结构 = 程序设计》，它正说明了数据结构在程序设计中的作用。程序设计的实质即为计算机处理问题编制一组"指令"，首先需要解决两个问题：即算法和数据结构。算法即处理问题的策略，而数据结构即为问题的数学模型。 　　很多数值计算问题的数学模型通常可用一组线性或非线性的代数方程组或微分方程组来描述，而大量非数值计算问题的数学模型正是本门课程要讨论的数据结构。 　　例一、求 n 个整数中的最大值。这似乎不成问题，但如果这些整数的值有可能达到1012，那么对32位的计算机来说，就存在一个如何表示的问题。 　　例二、交叉路口的红绿灯管理。如今十字路口横竖两个方向都有三个红绿灯，分别控制左拐、直行和右拐，那么如何控制这些红绿灯既使交通不堵塞，又使流量最大呢？若要编制程序解决问题，首先要解决一个如何表示的问题。 　　例三、煤气管道的铺设问题。如右图需为城市的各小区之间铺设煤气管道，对 n 个小区只需铺设 n-1 条管线，由于地理环境不同等因素使各条管线所需投资不同(如图上所标识)，如何使投资成本最低？这是一个讨论图的生成树的问题。 　　以上所举例子中的数学模型正是数据结构要讨论的问题。因此，简单地说，数据结构是一门讨论"描述现实世界实体的数学模型(非数值计算)及其上的操作在计算机中如何表示和实现"的学科。

很多问题求解最后都转化为求解数学方程或数学方程组，即使是不需要用计算机求解的简单问题也需要一个数学模型来描述，例如，大家都熟悉的"鸡兔同笼"问题，可转化为对"二元一次方程组"进行求解。又如在房屋设计或桥梁设计中的结构应力分析计算可化解为线性代数方程组求解的问题，再如，天天看到的天气预报，它的数学模型是一个环流模式方程。 　　而当计算机进入非数值计算领域、特别是用在管理上的时候，计算机的操作对象之间的关系就无法用数学方程加以描述了。