在关系模式R(U)中，设X，Y，Z是U的不同的属性子集，如果X→Y成立，且有
而有Y→Z成立，
则称Z传递函数依赖(transitive
functional dependency) 于X。式中XY表示是
。定义中说明
，是因为如果Y→X，则有
，实际形成X→Z是直接函数依赖，而非传递函数依赖。在STUDENT关系模式中，我们假定班级编号都与系的名称相关。例如：计算机系2000年入学的学生班级有6个，其班级名称为：JS001，JS002，JS003，JS004，JS005，JS006。这样一来，我们可以由学生的学号确定学生所在的班级，由班级名称就可以确定学生所在系，形成传递函数依赖：
SNO→SCLASS→SDEP
由定义中XY是指X∪Y，由此可以得到：
根据定义，可以证明，如果Z传递函数依赖于X，则Z函数依赖于X。
证明：设s, t是关系r中任意两个可能的元组，根据传递函数依赖条件可知：
如果s[X] = t[X], 则s[Y] = t[Y];
如果s[Y] = t[Y], 则s[Z] = t[Z];
由上可得：
如果s[X] = t[X], 则s[Z] = t[Z], 即X?Z。
说明：
X→Z并不是显式地表示出来的，而是从X→Y和Y→Z推导出来的。
5. 关系模式中的码
关系模式中有候选码，主码和外部码之分。在关系模型的介绍中，我们已经给出了有关术语的定义和说明。此处我们用函数依赖的概念对关系模式中的码再次给出定义。
（1） 候选码（Candidate key）
在关系模式R(U)中，K为R的一个属性或者一组属性，若满足K→U，则K为关系模式R的候选码(Candidate key)。
候选码是一组非空的属性名集合，每个属性必须为该关系模式的属性。
在关系模式R(U)中，包含在任何一个候选码中的属性称为主属性(prime Attribute)。不包含在任何候选码中的属性称为非主属性(Nonprime Attribute)或非码属性。
最简的情况下，单个属性是候选码。最极端的情况，所有的属性的组合构成码。如果整个属性组U是码，则称为全码。例如，在关系模式供应商（供应商名称，供应商地址，供应商电话）中，供应商名称是唯一的候选码。而在关系模式供应（供应商名称，供货名称，供应单价）中，属性的组合（供应商名称，供货名称）是唯一的候选码。
关系模式的每个候选码具有下列两个特性：
・ 唯一性：在关系模式R（U）中， 设K为关系模式R的候选码，则对于关系模式R的任何一个关系实例r中，任何时候都不存在候选码属性值相同的两个元组。即候选码的值唯一的决定元组的所有属性值，即r中的任意2个元组s和t，都有s[k]不等于t[k]
・ 最小特性：在不破坏唯一性的情况下，没有任何属性可以从候选码属性集中删除。即候选码是由其值唯一决定元组值的最小属性集组成。
例如：在供应关系中，必须由供应商名称和供货名称两者组合才能唯一的决定供应关系中的一个元组值，缺一不可。
下面给出一个具有多个候选码的例子。有关系模式CSZ(CITY,ST,ZIP)，其中有三个属性：城市为CITY，街道ST，邮政编码ZIP。其属性集合和属性间的函数函数依赖关系为：
U = { CITY,ST,ZIP }
F = {(CITY,ST)→ZIP,ZIP→CITY}
即城市和街道共同决定邮政编码，邮政编码决定城市。在这个关系模式中，有两个候选码，即（CITY，ST）和（ST，ZIP）。CITY，ST和ZIP都是主属性。
再给出一个全码的例子，如表5-2。我们有一个大部件的设计A，其中包含四个设计相同的左右并排放置的子部件，四个子部件的编号由左到右分别为I1,I2,I3和I4。设计一个关系模式描述四个子部件之间的左右邻接关系，关系模式左右邻接（左邻接部件，右邻接部件）。这个关系模式的唯一的候选码就是（左邻接部件，右邻接部件），即全码。
表 5-2
|
 |
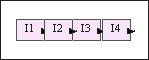在左右邻接关系中，必须由左邻接部件和右邻接部件共同决定其中的一个元组。
（2）主码(Primary Key)
在一个关系模式中，可以有多个候选码，但只能有一个主码。
若关系模式R(U)中有多个候选码，则选定其中的一个候选码作为主码，或称主关键字。
例如，在关系模式供应商（供应商名称，供应商地址，供应商电话）中，供应商名称是唯一的候选码，也是它的主码。而在关系模式供应（供应商名称，供货名称，供应单价）中，属性的组合（供应商名称，供货名称）是唯一的候选码，也是它的主码。在这个关系模式CSZ中，有两个候选码，即（CITY，ST）和（ST，ZIP），可以任选其中一个作为主码。在左右邻接关系中，关系模式的唯一的候选码（左邻接部件，右邻接部件）也是它的主码。
关系模式R中属性或属性组X并非R的候选码，但X是另一个关系模式的候选码，则称X是R的外部码（Foreign Key），也称外码。
例如：在供应关系模式中，供应商名称不是供应关系模式的码，但供应商名称是关系模式供应商的码，则称供应商名称是关系模式供应的外部码或外码。
主码和外部码提供了一种表示不同关系之间相互关联的手段。如关系模式供应商和供应之间的关系就是通过供应商名称来体现的。