无标题文档

��在下面的等价规则中，我们用θ、θ1、θ2等表示谓词；用L、L1、L2等表示属性列表；用E、E1、E2等表示关系代数表达式。
��⑴�合取选择运算可分解为单个选择运算的序列，该变换称为σ的级联：
��

��⑵�选择运算满足交换律：
��

��⑶�投影运算序列中只有最后一个运算是需要的，其余的可省略。该转换称为Π的级联：
　　　　

　　⑷　选择可与笛卡尔积以及theta连接相结合：
　　　　①　

，该表达式是theta连接的定义
　　　　②　

　　⑸　theta连接(包括自然连接)运算满足交换律：
��

　　⑹　自然连接运算满足结合律：
��(E1��E2)��E3 = E1��(E2��E3)
theta连接具有以下方式的结合律：
��

注意：其中q2只涉及E2与E3的属性。由于任意一个条件都可为空，因此笛卡尔积运算也满足结合率。
　　⑺　选择运算在下面两个条件下对theta连接运算具有分配律：
　　　　①　当选择条件q0的所有属性只涉及E1时：
��

　　　　②　当选择条件q1只涉及E1的属性，q2只涉及E2的属性时：
��

　　⑻　投影运算对theta连接运算具有分配律：
　　　　①�令L1、L2分别是E1、E2的属性，而连接条件θ只涉及L1∪L2中的属性，则：
��

��②�令L1、L2分别是E1、E2的属性，L3是E1里出现在连接条件θ中但不在L1∪L2中的属性，而L4是E2里出现在连接条件θ中但不在L1∪L2中的属性，那么：
��

��⑼�集合运算并与交满足交换律：
��E1∪E2 = E2∪E1E1∩E2 = E2∩E1但是集合差运算不满足交换律！
��⑽�集合运算并与交满足结合律：
��(E1∪E2)∪E3 = E1∪(E2∪E3)(E1∩E2)∩E3 = E1∩(E2∩E3)
��⑾�选择运算对并、交、差运算具有分配律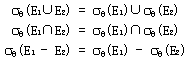
��

��⑿�投影运算对并运算具有分配率：
��ΠL(E1∪E2) = (ΠL(E1))∪(ΠL(E2))