��⑴�分布是均匀的：即每个存储桶从所有可能的搜索码值集合中分配到的值的个数差不多相同。这就是散列函数的均匀性；例如，假设搜索码值的可能集合为{A..Z}，而一共有5个存储桶，那么散列函数应该使每个桶分配到5个左右的搜索码；
��⑵�分布是随机的：一般情况下，不管搜索码值实际情况是怎样的，每个存储桶应分配到的搜索码值的个数也差不多相同。这就是散列函数的随机性，更确切地说，散列函数结果的分布不应与搜索码的任何外部可见的特性相关。例如，假设实际的搜索码值是{A,B,C,D,E}，那么散列函数应该使这5个存储桶中的每一个都分配到一个搜索码。
��下面我们看一个具体的例子：假设我们需要将26个大写英文字母分布到5个存储桶中(地址从0到4)，那么散列函数h该如何设计呢？
假设用code(A)表示A所对应的编号0，用code(B)表示B所对应的编号1，用code(C)表示C所对应的编号2，……
{A,B,C,…,Z}上的一个散列函数可以设计成：
��h = code(Search Key) mod 5
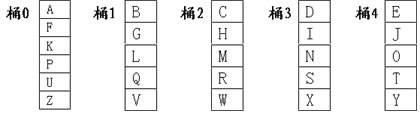
那么26个大写字母的分配如下图8-4-1所示：