示例��例1：
��如图5-5-1所示，关系r上函数依赖A→C是满足的，但C→A是不满足的；函数依赖AB→D也是满足的。注意，我们用AB作为{A,B}的简写。
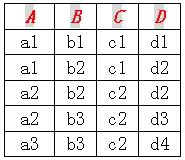
图5-5-1：数据库中的一个关系r
��有些函数依赖在所有关系中都是满足的，例如A→A和AB→A在所有包含属性A（及B）的关系中都是满足的。一般来说，如果βα，则形如α→β的函数依赖是平凡的，本章只讨论非平凡的函数依赖。对于平凡的函数依赖的证明可以采用以下简单的方法：
证明：因为βα，所以令α=β∪γ，然后再用函数依赖的定义进行证明即可。
例2：
　　假如有如下的关系模式：
Loan-info-schema = (branch-name, loan-number, customer-name, amount)
一般来说，我们希望在这个关系模式上有函数依赖集（即多个函数依赖组成的集合）：
loan-number→amountloan-number→branch-name
但是，不希望有函数依赖：
loan-number→customer-name
那么，这些要求的具体含义是什么呢？请大家自己思考。
��如图5-5-2所示，对于关系customer(Customer-schema)来说，函数依赖：customer-street→customer-city是满足的。但是对关系模式Customer-schema来说，上述函数依赖却不一定成立！因为不同的城市具有同名的街道是很可能的。
图5-5-2：关系customer
由此，我们可以得出结论：函数依赖a→b在关系r(R)上是满足的，但在关系模式R上不一定是成立的！