��1、问题的提出
��二元运算自然连接可以将某些选择运算和笛卡尔积运算合并为一个运算，用"连接"符号�±幢硎荆杭�r��s。自然连接运算的计算过程分解如下：首先，自然连接运算形成它的两个参数的笛卡尔积；接着在笛卡尔积的结果上，基于两个参数的关系模式中都出现的属性进行属性相等的选择运算；最后还要去除结果关系模式中的重复属性，即关系模式中相同的属性在连接结果中只保留一个。
��尽管自然连接的定义很复杂，但使用起来却很方便。例如，"找出所有在银行中有贷款的客户的姓名、贷款号和贷款金额"。用关系代数的基本运算可以表示如下：
而用自然连接运算就可以简单地表示如下：
 
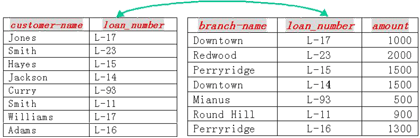
图3-2-11：参与自然连接运算的关系borrower和loan
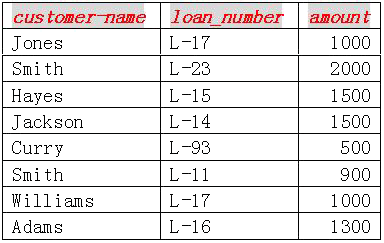
如上图3-2-11所示，由于关系borrower和loan的模式中都有相同的属性loan-number，自然连接运算只考虑在loan-number上值相同的元组对。而自然连接的结果模式为两个作为参数的关系模式的并，并的含义就是要去除重复属性，即：
��(customer-name, branch-name, loan-number, amount)
而作完投影运算之后，整个关系代数表达式的结果如图3-2-12所示：
图3-2-12：运算结果
��2、自然连接的形式化定义
��从上面的讨论可以看出，自然连接结果的关系模式是很重要的，为此我们要专门讨论一下。考虑两个关系模式R和S--它们都是属性名的一个序列。如果认为模式是属性的集合而不是序列，就可以用R∩S表示同时出现在R和S中的那些属性名集合；用R∪S表示出现在R中或S中或在二者中都出现的那些属性名集合。同样，出现在R中而不出现在S中的属性名集合用R-S表示，反之亦然。特别要注意的是这里的并、交、差运算都是建立在关系模式的属性集合上的，而不是关系上的。有了以上约定之后，就可以将自然连接运算形式化定义如下：设r(R)和s(S)是两个关系，r和s的自然连接表示为r��s，它是R∪S上的一个关系，具体定义如下：
其中R∩S = {A1,A2,…,An}。
��对于自然连接运算来说，它具有如下的性质和扩展：
��①关系代数表达式r �� s �� p与r �� (s��p)和(r��s) ��p是等价的，也就是说自然连接运算满足结合率；
��②设r(R)和s(S)是没有任何公共属性的关系，即R∩S=，那么r��s = rｘs；
��③theta连接是自然连接的扩展，它可以把一个选择运算和一个笛卡尔积运算合并为单独的一个运算。考虑关系r(R)和s(S)，并设Q是模式R∪S的属性上的谓词，则theta连接运算定义如下：。
��这里需要注意Theta连接和自然连接的区别。Theta连接是在笛卡尔积上进行选择运算，其结果关系模式的属性是参加笛卡尔积运算的两个关系的所有属性。而自然连接可以这样由Theta连接得到，首先进行笛卡尔积上的针对两个关系中所有相同属性的等值比较选择运算，然后再通过投影运算去掉结果中重复的属性，即两个关系中相同的属性在自然连接的结果关系模式中只出现一次。