|
��1、属性命名机制 |
|
��这种命名机制的一个缺陷就是要求参加笛卡尔积运算的关系名称必须不同。而当某个关系需要与自身做笛卡尔积时,这种命名机制就无能为力。
|
| ��2、笛卡尔积的元组 ��假设关系borrower中有n1个元组,关系loan中有n2个元组,那么可以有n1×n2中方式构成: |
|
r = borrowerxloan
|
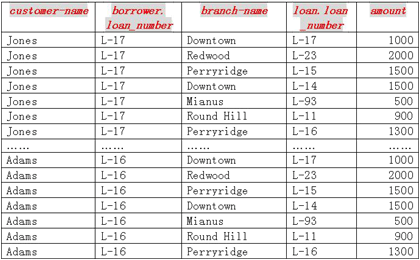
| 中的元组。也就是说borrower中的每个元组都要与loan中的所有元组进行配对,这样就构成了r中的全部元组。因此,r中应该有n1×n2个元组。特别要注意的是对于r中的某些元组t来说,可能会有: ��t[borrower.loan-number]≠t[loan.loan-number] |
|
图3-2-5:borrowerxloan的部分结果
|
| ��3、笛卡尔积的形式化定义 ��一般地,如果有关系r1(R1)和r2(R2),则关系r1×r2的模式是R1和R2串接而成的R。关系r(R)中包含所有满足下列条件的元组t:若t1∈r1,t2∈r2,则t由t1和t2拼接而成,且t[R1]=t1[R1],t[R2]=t2[R2]。 ��4、举例 ��假设要找出所有在Perryridge分支机构中有贷款的客户姓名,可以一步一步地分解如下: ��①�为实现这一要求,同时需要关系borrower和关系loan,这需要通过笛卡尔积将有关贷款关系的customer-name和branch-name连接起来: |
|
|
| 假设关系borrower和关系loan中的元组如下 |
|
图3-2-6:关系borrower和关系loan
.gif) .gif)
|
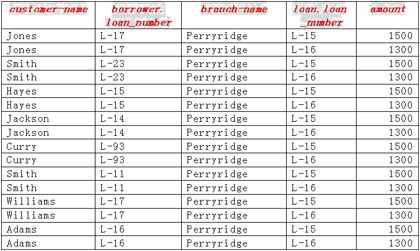
| 那么,上述关系代数表达式的计算结果如图3-2-7所示,表中所有的元组都与Perryridge分支机构有关: |
|
图3-2-7:在笛卡尔积的结果上进行选择运算的结果
|
| ��②�如果客户在Perryridge分支机构中有贷款,那么在borrower×loan中必定存在某个元组,这个元组具有如下性质: ��borrower.loan-number = loan.loan-number 因此,需要在①的结果(参见图3-2-7)的基础上继续进行选择运算: |
|
|
| ��③最后,由于我们只需要列出客户姓名,因此再对②的结果进行投影运算即可: |
 |
|
图3-2-8:最终结果

|