��1、表
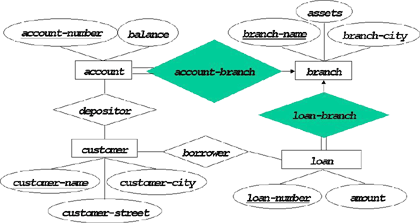
��关于表我们在2.9.1小节曾经提到过，那么什么又是关系数据库所说的表呢？为了充分理解表这个概念，首先让我们回顾一下作为本章基础的、一个简化了的银行企业数据库的E-R图
图3-1-1：银行企业数据库的E-R图
需要说明的是在图3-1-1中实体集customer可能包含在银行中既无帐户又无贷款的客户，同时为了简单起见取消了customer的social-security属性，而用customer-name作为customer的主码（假设不同的客户有不同的名字）。
��同样是在前面的2.9.2小节和2.9.4小节，我们学习了如何将强实体集和联系集转换为表的形式。根据图3-1-1的情况，将实体集account和联系集account-branch转换为如下两个表：
表account：具有列account-number和balance；
表account-branch：具有列account-number和branch-name；
由于联系集account-branch从account到branch是多对一的，而且实体集account全部参与了联系集account-branch，因此根据2.9.4小节中表的合并，可以得到合并后的新表account，如图3-1-2所示：
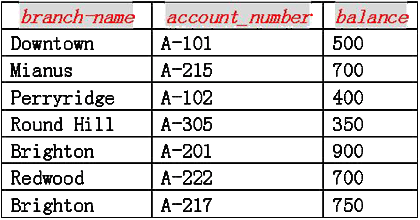
图3-1-2：account表
��从上面的例子和图3-1-2中可以看出，所谓关系数据库的表具有如下特征：
��①�每个表有唯一的名字；
��②�每个表可以有多个列；
��③�每个列有唯一的名字；
��④�表中的一行代表的是这些列之间的一个联系，而整个表的内容就是这种联系的集合。
��请看图3-1-2中的account表。该表有三个列首：branch-name、account-number和balance。用关系模型的术语讲，这些列首称作属性。每个属性有一个允许值的集合，称为该属性的域。例如，属性branch-name的域是银行所有分支机构名称的集合，我们用D1表示此集合。同理，可以用D2表示所有帐户号的集合，用D3表示所有可能余额的集合。
��2、表、关系与笛卡尔积
��account表中的每一行都必须是一个三元组（v1,v2,v3），其中v1∈D1，v2∈D2，v3∈D3。将account的所有可能行的集合称为D1、D2和D3的笛卡尔积，记作：D1′D2′D3。一般情况下，account表中所有行的集合是笛卡尔积D1′D2′D3的一个子集。因此，有n个属性的表是笛卡尔积D1′D2′...′Dn-1′Dn的一个子集。
��在数学上将关系定义为一系列域上的笛卡尔积的子集。这一定义与前面对表的定义几乎是完全相符的，从目前来看，唯一的区别在于我们给表中的属性赋予了名称，而关系则没有。由于表实际上就是关系，因而在关系模型中，用数学名词关系和元组来代替表和行。
��3、属性值的表示
��如图3-1-2所示关系account中共有7个元组。假设元组变量t指向关系中的第一个元组，那么t[branch-name]就表示t在branch-name属性上的值，因此t[branch-name]="Downtown"，t[balance]=500；当然也可以用t[1]来表示元组t在第一个属性branch-name上的值，因此t[1]="Downtown"，t[2]="A-101"。同时，由于关系是元组的一个集合，因此我们采用数学上的表示法t∈r表示元组t在关系r中。
��4、域
��对于"域"的概念来说，需要注意以下几点，
��第一：对所有关系r而言，r的每个属性的域都应是原子的，即不可再分割的（如果域的元素被看作是不可再分的单元，则域是原子的）。例如整数集合就是一个原子域。最重要的问题不在于域自身是什么，而在于如何在数据库中使用域中元素，如字符和字符串；
��第二：有时几个属性会有相同的域。例如customer-name和employee-name的域就可能相同，都是所有人名的集合，而balance和branch-name的域则显然不同；
��第三：值null是所有可能域的成员，表明值未知或不存在。