��图8.30是一个Mip-mapping纹理金字塔的定义域,它被均匀地分为四份,其中RGB三基色各占一份,存放初始的纹理图像。另一份(左下角)又被均匀地分割为四小份,每一份都是分割前的四分之一,其中三分分别存放纹理图像的RGB值,其分辨率与分割前的纹理图像的分辨率之比为1:4。剩下的左下角的一份继续分割,直到只有一个单元为止。这个过程相当于为纹理图像的三基色RGB建立了一个金字塔。纹理图像RGB金字塔的每一层都是分别定义在单位正方形上(即:纹理坐标(u,v)∈[0,1]×[0,1])的被压缩过(第0层除外)的RGB(三个)纹理图像,通常第i层的每个纹理图像与第i-1层的分辨率之比为1:4,相对于第0层的分辨率之比为1/4i。Mip-mapping金字塔的全部信息作为一个纹理查找表存储于二维数组中,所需的内存大小是原有图像的内存的(1+1/4+1/16+1/64+…)=4/3倍。 ��例如,一个256×256的纹理图像,用512×512个字节存放,这是一个9层的金字塔(从第0层到第8层)。第i层纹理图像是原始纹理图像经过用一个长为2i( 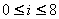 )个像素的方形滤波器滤波后得到的。金字塔的最底层为第0层,存放256×256个像素的原始RGB纹理图像,金��字塔的最顶层为分别只有一个像素的RGB图像,是整个原始纹理图像与边长为256个像素的滤波器卷积后得到的压缩图像。 )个像素的方形滤波器滤波后得到的。金字塔的最底层为第0层,存放256×256个像素的原始RGB纹理图像,金��字塔的最顶层为分别只有一个像素的RGB图像,是整个原始纹理图像与边长为256个像素的滤波器卷积后得到的压缩图像。��Mip-mapping纹理查找表是靠三个参数(u,v)和d来访问的,如图8.31所示。(u,v)是二维纹理图像的坐标,d是压缩比,可以看成是金字塔竖直方向上的坐标。假设一个屏幕像素映射到原始纹理空间的区域的面积为Auv(见图8.28右上角附近的阴影区域, 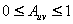 ),则压缩比定义为 ),则压缩比定义为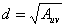 ,
, 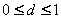 。 。
��由于纹理坐标u和v的变化范围都是0~1,对于一个256×256的纹理图像来说, 一个像素的面积就是(1/256)×(1/256)=1/216,金字塔的第i层纹理图是对原始纹理图用边长为2i个像素的盒状滤波器滤波后得到的,这等价于原始纹理图中的2i×2i=22i个像素压缩到第i层中的一个像素,因此,第i层纹理图像中的一个像素的面积为: 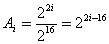 。
。于是,第i层纹理图像的压缩比为 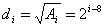 , ,
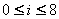 。 。��假定初始纹理图像的分辨率为n×n,则Mip-mapping纹理金字塔的层数为 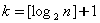 ,原始纹理图像中一个像素的面积,金字塔的第i层纹理图像的压缩比为 ,原始纹理图像中一个像素的面积,金字塔的第i层纹理图像的压缩比为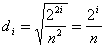 , ,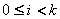 。
。 它是一个实数,而且 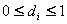 。 。��如果已知一个屏幕像素在纹理空间中的映射区域(多边形,简称纹理映射区域),如图8.28所示,则(u,v)近似地取作这个区域的所有顶点坐标的平均值,d取为这个区域的面积Auv的平方根。这实际上是用中心在(u,v)、与纹理映射区域的面积相等的一个正方形替代了这个纹理映射区域。实践证明,在绝大多数情况下,这种替代所产生的误差可以忽略不计。 ��有了三个参数(u,v)和d之后,我们就可以通过查表来决定该屏幕像素的颜色值了。由于Mip-mapping纹理查找表中只存储了有限种分辨率下对纹理图像的采样结果,即只有当 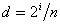 (i=0,1,…,k)时,以d为边长的正方形区域才与Mip-mapping纹理金字塔的第i层的基本采样单元相匹配。换句话说,只有当Auv正好等于 (i=0,1,…,k)时,以d为边长的正方形区域才与Mip-mapping纹理金字塔的第i层的基本采样单元相匹配。换句话说,只有当Auv正好等于
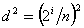 时,第i层纹理图中的一个像素的面积才正好等于Auv。此时,如果(u,v)位于第i层纹理图中的某个采样点处,即位于某一基本采样单元(像素)的中心时,可以从纹理查找表中直接查出该像素的纹理颜色值,它就是该纹理映射区域的平均纹理颜色。但是,一般来说,d为一任意实数。当di<d<di+1时,可以通过第i层和第i+1层的线性插值来得到任一中间分辨率的纹理图像: 时,第i层纹理图中的一个像素的面积才正好等于Auv。此时,如果(u,v)位于第i层纹理图中的某个采样点处,即位于某一基本采样单元(像素)的中心时,可以从纹理查找表中直接查出该像素的纹理颜色值,它就是该纹理映射区域的平均纹理颜色。但是,一般来说,d为一任意实数。当di<d<di+1时,可以通过第i层和第i+1层的线性插值来得到任一中间分辨率的纹理图像: |