1. 假定视点及单一点光源均位于z轴正无穷远处。分别采用Gouraund和Phong的明暗处理方法,以及Phong明暗处理快速方法,显示正20面体。
2. 假设在完成习题1所要求的显示前,视点与点光源已分离,前者位于(1,1,1,0),后者位于(-1,1,1,0)。另外,该正20面体已位于z=0平面上。试按习题1的要求并且加上阴影显示该场景。
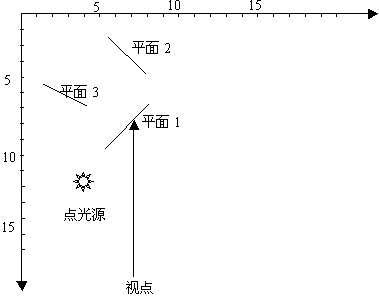
3. 如图所示,场景中的显示对象为三个与x-z平面垂直的不透明的平面构成,交线已经在图上画出。这三个平面的方程分别为:
��平面1是:x+z-12.5=0 (4≤x≤6)
��平面2是:x-z-2=0 (4≤x≤6)
��平面3是:x-3z+9=0 (1≤x≤3)
��另外,每一平面的光照特性为
��平面1:ka1=0.15,kd1=0.15,ks1=0.8,kt1=0.5,kμ1=1.1
��平面2: ka1=0.15,kd1=0.15,ks1=0.8,kt1=0.5,kμ1=(1.1)-1
��平面3: ka1=0.15,kd1=0.15,ks1=0.8,kt1=0,kμ1=(1.1)-1
��4. 以你的教室为场景,并在面对讲台的墙中间再添加一面镜子,其大小为墙的1/9。用光线跟踪算法绘制该场景的真实感图形。