2） 球面环境映射
��环境映射是Blinn和Newell在1976年首先提出来的。他们假定环境是由遥远的景物和光源组成，并忽略待绘制的物体遮挡部分环境的情况。其基本思想是：首先，以待绘制物体的中心为球心建一个大球（称为环境球），球面的参数方程是一个由经纬坐标 决定的二维函数。以球心为视点，以该球面的内侧为投影面，绘制所有的环境物体，这样，我们就可以得到一幅球面上的环境纹理图像。然后，在绘制物体时，从视点出发经过每个像素的四个顶点的光线到达待绘制的物体表面后产生反射（见图8.24），反射光束再与环境球面相交，即可得到环境纹理中的相交区域，最后将这部分相交区域的环境图像作为纹理映射到待绘制物体的表面。1993年，Haeberli和Segal对环境映射进一步进行了研究，将单位球的半个球面上的环境图像在二维纹理平面上进行编码，提高了环境映射的效率。
��为了简化计算，提高计算效率和图像质量，通常对环境图像预先作滤波处理，并以二维编码的形式进行存储，使得景物表面上任意一点的纹理信息能够简单地通过编码进行快速查找，而不必计算反射光线与环境球面的交点。为此，我们仅用反射光线向量R来实现其编码，即构造一条以球心C为起点、且平行于R的射线，取该射线与环境球面的交点E?处的纹理图像作为P点处的纹理。编码的关键在于如何快速地计算纹理坐标（s，t）。
��如图8.24所示，设P点处的单位法向量为N，单位反射向量为R，则

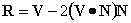
其中V是从视点指向P点的单位向量。
��图8.25是用于计算纹理坐标的一个横截面图。环境球的半径等于1，球心位于坐标原点。假设视点位于无穷远处，视方向为K＝（0，0，1），光线的方向用单位矢量R＝（Rx，Ry，Rz）表示，光线与球相交于点E＝（x,y,z）^T，在这个交点处的单位法矢量N＝（x,y,z）^T，由于入射角等于反射角，所以单位矢量K，N和R共面，且N位于K和R的角平分线上，换句话说，N正比于K和R的矢量和，即：，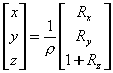

其中，
。
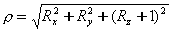于是，（x,y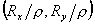）= 。假定纹理图像的x和y的范围均从－1到＋1，我们想在球面上的P点看到的被反射的东西，就是二维纹理图像中在（x,y）点处的颜色值。
��通常，我们总是把纹理图像的坐标范围限制在0～1之间。那麽，我们希望在点（x,y）处所看到的就是在纹理坐标（s,t）处的纹理图像的颜色值，其中纹理坐标（s,t）用下式计算：
，
。
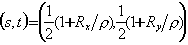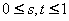��上述分析可以用于指导我们生成一幅二维的环境纹理图像，然后，令纹理坐标（s,t）的范围为0～1。在进行环境映射时，把视线与待绘制物体表面的交点处的反射单位向量带入上式，便可以得到纹理坐标（s,t）的值，从而可以避免计算反射单位向量与环境球面的交点，提高算法的效率。下图就是Haeberli和Segal1993年给出的一个环境映射的例子。