| ��曲面S(u,v)上任意一点处的法向量可通过沿u、v两个方向的偏导矢量的叉积得到: �� 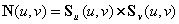 。 。��定义一个随机的扰动函数F(u,v),使理想光滑表面上的每一个点S(u,v),都沿该点处的法向量方向移动F(u,v)个单位长度,这样新的表面位置变为: 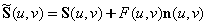 , ,其中, 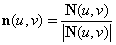 。 。新表面的法向量可通过沿u、v两个方向的偏导矢量的叉积得到: 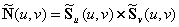 。 。而偏导矢量 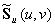 和 和
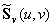 为 为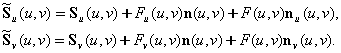 由于扰动函数F(u,v)的值相对于上式中其他的量很小,因此上两式的最后一项可以忽略不计,于是有 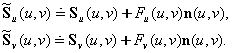 所以,新表面的法向量为 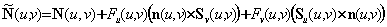 。 。��上式右边的最后两项可以看成是原曲面法向量的扰动项。扰动后的法向量单位化后,用于计算曲面的亮度,可以产生貌似凹凸不平的几何扰动纹理。图8.27是一个一维情况下几何扰动纹理映射的例子。 ��扰动函数F(u,v)可以任意选择,它可以是用数学函数定义的简单的网格图案、字母位图或其它的彩色位图。其偏导数的计算,如果F(u,v)不是用解析函数表示的,可以用中心差分实现。当采用彩色纹理图案定义F(u,v)时,几何扰动纹理函数的定义与颜色纹理的定义方法相同,可以用统一的图案纹理记录,图案中较暗的颜色对应于较小的F(u,v)值,较亮的颜色对应于较大的F(u,v)值,把各象素的值用一个二维数组记录下来,用几乎类似于二维纹理映射的方法映射到物体表面上,就可以成为一个几何扰动纹理映射。 |