��（2） 球映射
��将一个矩形平面映射到整个曲面上时,在球的两个极点附近会产生严重失真。在此，我们仅仅考虑将纹理映射到如图8.20所示的部分球面的情形。
图8.20 部分球面的纹理映射

��设球表面的参数为（u,v）=（θ，）， （0≤θ≤π/2, π/4≤φ≤π/2），在三维直角坐标系中，球表面的参数方程为：
��
我们用如下线性变换将纹理映射到球的表面：
（8－9－2）
��
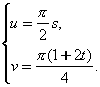
其中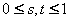， ，s和t是纹理平面的参数，如图8.19左上角所示。
然后，采用某种真实感图形绘制算法（如：光线跟踪）生成该球面的真实感图形。球面上的任一点P（u,v）到纹理空间T（s,t）的映射关系为：

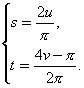
��将被每个象素区域所覆盖的矩形纹理图案中的光亮度值取平均，把该平均值作为圆柱表面上P点的漫反射系数Kd代入光照明模型进行计算，最后就能够生成该带有纹理图案的球面的真实感图形。

��（3） 两步映射
��在前面的例子中，为了进行纹理映射，需要对三维的景物表面进行参数化，以便建立三维表面到二维纹理平面的映射关系。可以看出，对景物表面参数化的方法不同，所得到的纹理映射的结果一般也不同。1986年Bier和Sloan提出了一种两步纹理映射技术，他们引入一个中间过渡表面，将纹理映射过程分解成为两步操作：纹理平面→过渡表面→景物曲面。
��a） 将二维的纹理空间映射到一个包含景物的过渡表面，该过渡表面通常是比较简单的三维表面，例如：平面、圆柱面、球面和立方体。即：建立一个从纹理空间到三维过渡表面的映射：
��T(u，v) → T(x′，y′，z′)，
��称之为S映射。
��b） 将将三维过渡表面上的纹理映射到目标景物的表面，即：建立一个从三维过渡表面到目标景物表面的映射：
��T(x′，y′，z′) → O(x, y, z)，
��称之为O映射。
��在S映射中，过渡表面的选择主要取决于目标景物表面的形状。不同的过渡表面所生成的纹理效果也不相同。
��对于O映射，可选择以下四种映射方式，如图8.21中（a）、（b）、（c）、（d）所示：
��a） 景物表面上的点P(x,y,z) 处的纹理，取反射光线与过渡表面交点处P′的纹理。
��b） 景物表面上的点P(x,y,z) 处的纹理，取该点的法向量与过渡表面交点P′处的纹理。
��c） 景物表面上的点(x,y,z) 处的纹理，取物体中心到该点的连线与过渡表面交点P′处的纹理。
��d） 景物表面上的点P(x,y,z) 处的纹理，取通过该点且垂直于过渡表面的切平面的直线与过渡表面的交点P′处的纹理。

图8.21 四种O映射： (a) 反射光线，(b) 面法向量，(c) 景物中心线，(d) 过渡面法向量

��在O映射的四种映射方式中，第一种映射方式实际上就是所谓的环境映射。其余的三种O映射和四种S映射可以有12种组合，但是只有5种组合可以实际应用：第三种O映射（见图8.21c）可以和以立方体或球面作为过渡表面的S映射组合，而第四种O映射（见图8.21d）可以和以平面、圆柱面或立方体作为过渡表面的S映射组合。