|
��1)
球面
��设球心为 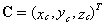 ,半径为r,则其方程为: ,半径为r,则其方程为:
��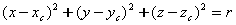
将光线的参数方程方程代入上式,经整理得到:
��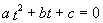
其中,
��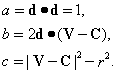
��如果b2-4c<0,则光线与球无交。
��如果b2-4c=0,这时t=-b/2,如果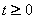 ,切点
,切点 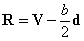 即为光线与球的交点,否则交点不在光线上。 即为光线与球的交点,否则交点不在光线上。
��如果b2-4c>0,这时 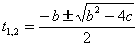 ,若有t1或t2<0,则说明相应的交点不在光线上,交点无效。取 ,若有t1或t2<0,则说明相应的交点不在光线上,交点无效。取
 ,则光线与球的交点为R(t0),交点处的法向量为 ,则光线与球的交点为R(t0),交点处的法向量为
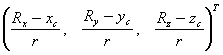 ,这是一个单位向量。 ,这是一个单位向量。
��用上述代数法计算光线与球的交点和法向量总共需要17次加减运算、17次乘法运算、1次开方运算和3次比较操作。如果采用几何法计算光线与球的交点和法向量,可以适当减少计算量,这里从略,建议读者自己练习之。
��2) 参数曲面
��设参数曲面的参数方程为:
��Q(u,v)=(x(u,v),y(u,v),z(u,v) )。
��假设光线的单位方向矢量d=(dx, dy, dz)T与光线起点的位置矢量V=(Vx, Vy, Vz)T不平行。这里,我们将用下面两个平面的交线来表示光线:
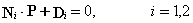
其中,
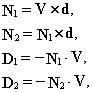
P=(x,y,z)T为平面上的一点 。如果d平行于V,则用不平行于d的某一坐标轴矢量取代上式中的V。
光线与参数曲面的交是下列非线性方程组的解:
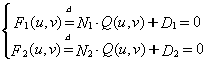
��采用Newton迭代算法求解:
��1) 给定初始值(u0, v0),令k=0;
��2) 将上式在(uk, vk)处作线性展开:
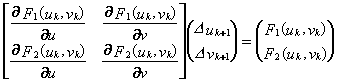 。 。
��通常上式左边的雅可比矩阵是非奇异的,所以有唯一解。
��3) 解上述线性方程组,得 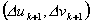 ; ;
��4) 如果
��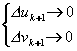
��转6);否则转5);
��5) 令
��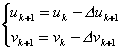
��转4);
��6) 结束。
��将Newton法所求得的解(uk+1,vk+1)代入曲面方程,即得交点Q(uk+1,vk+1)。
|