7.4 深度缓存(Z-buffer)算法 ��深度缓存算法是一种图象空间的消隐算法，它需要二个数组：一个是深度缓存数组ZB（Z-buffer，又称为Z缓冲器），另一个是颜色属性数组CB (Color-Buffer，又称为帧缓冲器)，这两个数组的大小和屏幕上显示图形的区域（即视口）的大小有关，等于视口的宽度（横向象素数）m和高度（纵向象素数）n的乘积。其基本思想和消隐过程是：首先给深度缓存数组中的每个单元赋初，如果视点的方向是Z轴的反反向，一般取初始值为z的最小值；颜色属性数组中的每个单元的初值可设成背景颜色的值。图形消隐的过程就是决定Z缓冲器和帧缓冲器中相应单元的深度和颜色值的过程。通过扫描转换，依次把每一个面离散成为象素点，逐个将象素点的深度值（z坐标值）和Z缓冲器中相应单元的值进行比较，如果前者大于后者，则用当前象素点的颜色值替换帧缓冲器的相应单元的颜色值，同时Z缓冲器中相应单元的值也要改成当前这个象素点的z坐标值。反之，如果这点的z坐标值小于Z缓冲器中的值，则说明对应象素已经显示了对象上一个点的属性，该点要比当前考虑的点更接近视点。因此，保持Z缓冲器和帧缓冲器中的值不变。处理完显示对象的所有面之后，帧缓冲器中便得到了消隐输出的图形。 ��这个算法的关键在于，要尽快计算出多边形内的点及其深度值。这里需要应用多边形中的点与点之间的相关性，包括水平相关性和垂直相关性。我们先来分析多边形中相邻的点的深度值在水平方向上的相关性。 ��设某个多边形所在的平面方程为： ��ax+by+cz+d=0， 若c不为0，则 ��z=－(ax＋by＋d)/c。 在点（xi,yi）处， ��zi = －(d＋axi＋byi)/c。 而在点（xi+1,yi）处 ��zi+1 = －(d＋axi+1＋byi)/c 因为逐点扫描时，xi+1 = xi + 1，所以 （7－4－1） �。 ��这个公式表明：在平面多边形中，点的深度值在水平方向x上可以递推计算。对于确定的面片，－a/c是一个常数，所以沿水平扫描线的后继点的深度值，可以由前面点的深度值执行一次加法获得。 ��类似地，可以得到平面多边形内的点的深度值在垂直方向y上的递推关系： 假定多边形的左边界线在视平面上的投影线的斜率为k，我们在y方向上，从上到下扫描，即yi+1 = yi -1，则扫描线与左边界线的投影的交点的x坐标： ��xi+1 = xi - 1/k， 沿该边的深度值也可以递归的计算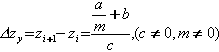： �� 如果是沿一条垂直边进行处理，这时由于斜率为无穷大，则上式可以简化为： ��。