二、直线与多边形的交点
��直线段与多边形的交点的个数，等于它与多边形的所有的边的交点数之和。这似乎是一个简单的问题，但是有两种特殊情况需要处理：
��（a）直线与多边形的顶点相交
��如果直线ab与多边形的两条边P_iP_i＋1 和P_i＋1P_i＋2的交点Q非常接近P_i＋1，即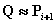 ,这时，我们还需要测试这两条边P_iP_i＋1 和P_i＋1P_i＋2的另外两个端点P_i和P_i＋2是位于直线ab的同侧还是异侧。如果是前者，如图7.7（a）所示，则认为P_iP_i＋1 和P_i＋1P_i＋2与直线ab无交点；如果是后者，则认为P_iP_i＋1 和P_i＋1P_i＋2与直线ab有一个交点，见图7.7（b）。

��（b）直线与多边形的某条边重合
假定直线ab与多边形的一条边P_i＋1P_i＋2 重合,这时，我们需要进一步测试与这条边首尾相连的两条边P_iP_i＋1 和P_i＋2P_i＋3的另外两个端点P_i和P_i＋3是位于直线ab的同侧还是异侧。如果是前者，如图7.7（c）所示，则认为P_iP_i＋1 、P_i＋1P_i＋2和P_i＋2P_i＋3这三条边与直线ab无交点；如果是后者，则认为P_iP_i＋1 、P_i＋1P_i＋2和P_i＋2P_i＋3这三条边与直线ab有一个交点，见图7.7（d）。

��综上所述，我们可以统一处理上述2种特殊情况：
��（a）如果多边形的边与直线平行，那麽它们无交点；
��（b）当直线与多边形的边的某一端点相交时，如果多边形的边位于直线的左侧，则忽略该交点（与该边的交点数记为0），如果多边形的边位于该直线的右侧，则认为该交点有效（与该边的交点数记为1，总的交点数增加1）。