二、NURBS曲线在齐次坐标系下的几何意义 ��首先，让我们考虑平面NURBS曲线的情况。如图6.13所示，给定一组控制点的二维坐标（xi, yi）及其权因子ωi，在齐次坐标系xyω 中可以表示为 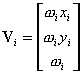，i=0,1,…,n；节点矢量 ， 。齐次坐标下的k阶非有理B样条曲线可表示为： �� ��若以坐标原点为投影中心，把C（t）投影到ω＝１的平面上，如图6.13所示，则得到平面曲线 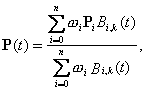这就是一条二维k阶NURBS曲线。 ��三维空间的NURBS曲线可以类似地定义。即对于给定的一组控制点及其权因子，则有相应的带权控制点，在四维空间xyzw中定义了一条四维的k阶非有理B样条曲线，然后，取它在ω＝１ 的超平面上的中心投影，即得三维空间里定义的一条k阶NURBS曲线。 ��这里不仅描述了NURBS曲线的几何意义，也说明：非有理B样条曲线的算法可以推广到NURBS曲线，只不过是在齐次坐标系下进行。实际上，对于后面即将介绍的NURBS曲面，也存在着类似的情况。