（1） 局部性   在k阶NURBS曲线上任一点的位置至多与k个相应的控制点及其权因子有关，与其它的控制点和权因子无关；另一方面，如果改变k次NURBS曲线的一个控制点Pi或权因子 ωi，仅仅只影响至多k个曲线段的局部形状。即：当Piωi 变化时，仅仅影响t∈[ti,ti+k) 区间内的一段曲线。 （2） 凸包性   如果ωi≥0,i=0,1,∧,n，定义在非零节点区间上的曲线段总是位于定义它的k个控制点的凸包内；整条NURBS曲线位于所有定义各曲线段的控制顶点的凸包的并集内。如果某个权因子小于0，则不能保证凸包性成立。 （3） 几何不变性   NURBS曲线的形状和位置与坐标系的选取无关。 （4） 变差缩减性   设NURBS曲线C（t）的控制多边形P0, P1, P2, …., Pn（n≥k－1）是一平面折线，在该平面内的任一直线与C（t）的交点的个数不多于该直线与其控制多边形的交点个数。 （5） NURBS曲线具有仿射变换不变性。     （6） NURBS曲线与有理基函数具有相同的可微性。     （7） 如果某个权因子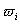为零，那么相应的控制点Pi对曲线的形状等几何特性没有影响。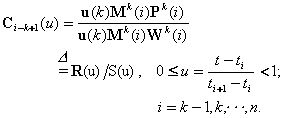     （8） 任意r（r≥1）阶导数   利用B样条基函数的局部支撑性，NURBS曲线C（t）可以用矩阵的形式表示如下： �� 其中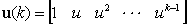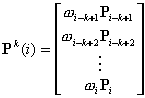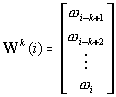， ��， ��， ��。 Mk(i)是k阶基矩阵。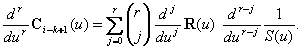 用矩阵公式表示的NURBS曲线的r阶导数为： � 经常使用的是NURBS曲线的一阶和二阶导数： �， � �. ��������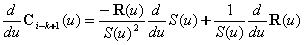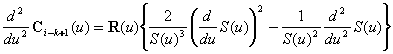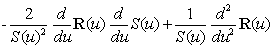