三、B样条曲线的定义：     给定三维空间的n＋1个控制点P0，P1， P2，…，Pn（n≥k－1），节点矢量由节点的一个非减序列 构成，称下列参数曲线�左（6－4－2） 为定义在T上的k阶（k-1次）的B样条曲线。折线P0，P1， P2，…，Pn为P（t）的控制多边形。     令节点数为m，则节点数m、控制顶点数（n+1）和曲线的阶数k三者之间的关系为：m=n+k+1。     考虑到B样条基函数的局部性质，（6－4－2）式可以改写为�左（6－4－3）     如果节点矢量的两端点是k重节点，即 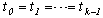, �� 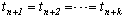, 那么,由（6－4－2）或（6－4－3）式所定义的曲线被称为端点插值B样条曲线。端点插值B样条曲线的两端点与控制多边形的首末端点重合。     如果 ，i＝0，1，…，n+k-1，其中c为某一常数（实数），则该曲线称为均匀B样条曲线。     如果 , , 并且 ，i＝k-1，k，…，n，则该曲线称为准均匀B样条曲线。