|
十、B样条曲线的降阶
为了实现不同CAD系统之间的产品数据交换,曲线的降阶逼近技术是常用的基本工具。一般而言Bézier曲线的降阶比B样条曲线的降阶要简单一些。1995年,Piegl和Tiller先将B样条转换成为一系列的Bézier曲线,然后对各条Bézier曲线进行降阶,最后再把他们拼接成B样条曲线并去除多余的重节点。1998年Wolters等将B样条曲线升阶的开花(blossom)算法的公式用于B样条曲线的降阶,并对曲线进行光顺设计。这些算法的逼近误差通常都比较大。
��下面,我们首先给出B样条曲线退化的充要条件,然后利用B样条升阶恒等式,导出B样条曲线降阶的算法,最后并对降阶后的曲线进行误差分析。
6.4.1.10.1 B样条曲线可降阶的充要条件
B样条曲线是一种分段连续曲线。给定曲线的n个控制点Vi(i=0,1,...,n-1) 和节点ti(i=0,1,...,n+k-1),节点矢量T=
{t0 t1 ... tn+k-1}。
当t∈[tj+k-1,tj+k) 时,k阶B样条曲线可以表示为 ck(t)=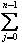 VjBj,k(t),或者: VjBj,k(t),或者:
��左(6-4-19)
其中,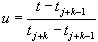 ∈[0,1),Bi,k(u)
为k阶B样条基函数, Mk(i)为该曲线在t∈[ti,ti+1]时的k×k
阶基矩阵,该基矩阵可以由递推公式(6-4-5)求出。 ∈[0,1),Bi,k(u)
为k阶B样条基函数, Mk(i)为该曲线在t∈[ti,ti+1]时的k×k
阶基矩阵,该基矩阵可以由递推公式(6-4-5)求出。
显然,曲线ckj(u)可降阶的(又称为退化的)充要条件为ckj(u)=cjk-1(u)
,其充要条件可以表示为:
��左(6-4-20)
对曲线的控制顶点Vi选取适当的扰动εi,使得扰动后的曲线
��左(6-4-21)
满足退化条件:
��左(6-4-22)
取所得曲线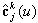 为 ckj(u)的降阶逼近曲线。由于扰动后,该曲线的次数已由(k-1)降到(k-2),因此扰动后的曲线可以准确的降为k-1阶。
为 ckj(u)的降阶逼近曲线。由于扰动后,该曲线的次数已由(k-1)降到(k-2),因此扰动后的曲线可以准确的降为k-1阶。
|