四、B样条曲线的性质
1）局部性
因为B_i,k(t)只在区间[t_i, t_i+k)中为正，在其它地方均取零值，使得k阶的B样条曲线在某点处的形状只与相关的k个控制点有关，而与其它控制点无关。当移动B样条曲线的某一个控制点P_i（0≤i≤n ）时，只对其中的一部分曲线（对应于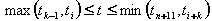

的那一段）产生局部影响，并不对曲线的其它地方产生影响。

2）连续性或可微性
B样条曲线P（t）在r重节点处的连续阶不低于k-r-1；整条曲线的连续阶不低于k-r_max-1。其中r_max是位于区间[t_k-1, t_n+1]内的节点的最大重数。
B样条曲线在每一曲线段内部是无限次可微的。

3）凸包性
B样条曲线在区间[t_i, t_i+1]上的部分曲线位于P_i-k+1，P_i-k+2，…， P_i的凸包之内；整条曲线位于该曲线的所有控制点的凸包之内。

4）几何不变性
B样条曲线的形状和位置与坐标系的选取无关。

5）变差缩减性
设B样条曲线P（t）的控制多边形P₀, P₁, P₂, …., P_n（n≥k－1）是一平面折线，在该平面内的任一直线与P（t）的交点的个数不多于该直线与其控制多边形的交点个数。

6）分段多项式
P（t）在每一长度非零的区间（t_i， t_i+1）上，n≥i≥k－1都是次数不高于k-1次的、以t为参数的多项式，P（t）是参数t的k-1次的分段多项式曲线。

7）仿射不变性
对任一仿射变换A：
,。
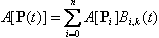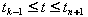即在仿射变换下，B样条曲线P（t）的表达式具有形式不变性。