一般地，对于一条有m个控制点的ｋ阶非均匀B样条曲线(m>k),设其节点矢量为，

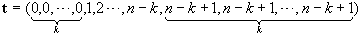
插入重节点后，新的节点矢量为：
。
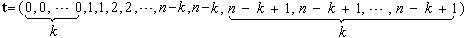    设插入重节点后的曲线有ｎ个控制顶点（在上例中，n=m*2-k），则该曲线可以分为n-k+1段，分别表示为C^k_j(u),j=0,1,...,n-k，对其控制点V_i 选取适当的扰动ε_i，使得每段修正曲线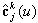 都满足退化条件（6－4－22）。
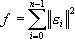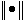令 ，其中 为Euclid范数。
由约束优化方法，可以由下式来确定ε_i：
，
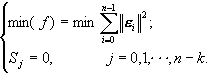取Lagrange函数为
L =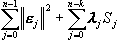
则有
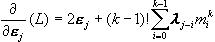(j-i+k-1)=0, j=0,1,...,n-1, （6－4－23）
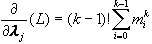(j+k-1)(V_j+i+ε_j+i)=0, j=0,1,...,n-k, （6－4－24）
其中,m^k_j(i)(j=0,1,...,k-1) 由下式定义
M_k(i)＝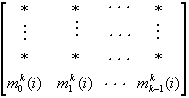
    由于节点距为0的曲线段所对应的S_j≡0 ，相应的这些约束方程可以不考虑。此外，为了使降阶后的曲线与原曲线具有相同的端点，应加入边界条件ε₀=ε_n-1=0 。整理后可得以下方程：
（6－4－25）

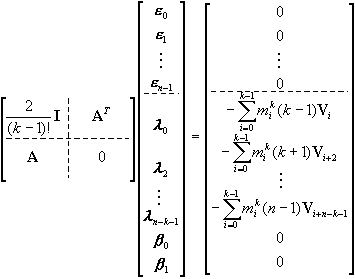
其中，Ｉ为n阶单位矩阵，
A=
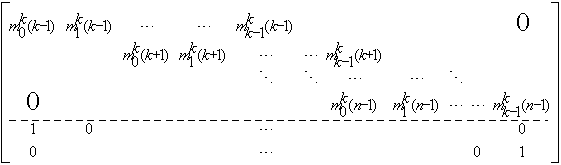