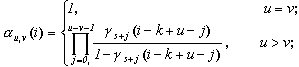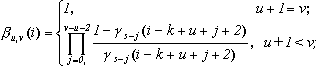定理1 非均匀B样条基函数满足以下恒等式: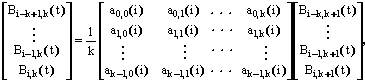 （6－4－14） . 式中 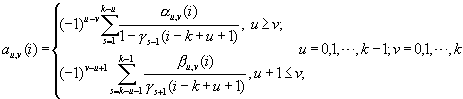（6－4－15） 利用B样条的权性质, 容易证明: 定理2 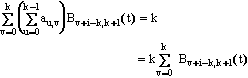（6－4－16） ��, v=0,1,…,k. 证明: 由于 , 当 时, 由式（6－4－14）得: ��� 比较上式两边的系数即得式（6－4－16）。证毕。     定理1清楚地表明了k阶与 k+1阶B样条基函数之间的关系。利用这一关系, 很容易得到B样条和NURBS等曲线的升阶公式和算法。     设k阶B样条曲线的控制顶点为Vj(j=0,1,…,n), 节点矢量为U= , 则B样条曲线的方程为 （6－4－17） ��Ci-k+1 (t) = [Vi] T Ni(t), i = k-1,k,…,n-k+1 � 其中, ��Vi = [Vi-k+1, Vi-k+2, …, Vi] T, ��Ni (t) = [B i-k+1, k(t), B i-k+2, k(t), …, Bi, k(t)]T。