|
1) 一阶几何连续
所谓一阶几何连续,就是指切线共线。根据Bezier曲线的端点条件:
其连续条件为:
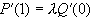 ,
, |
即
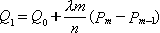 。 。 |
其中,λ为任意实数。其几何意义表示:
为使达到一阶几何连续性,曲线的控制顶点应当满足:Pm=Q0,而且Pm-1、Pm和Q1必须共线。
2) 二阶连续性
根据二阶导矢量:
为满足连续性条件:
可得:
几何意义: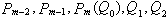 共面。
共面。
实际上,通常要求达到二阶几何连续即可满足要求。满足二阶几何连续性的充要条件是:
��I.Pm=Q0。
��II. 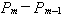 和 和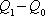 均不为0,且同向。
均不为0,且同向。
��III.在Pm处曲率相等且主法线的方向一致。即:
��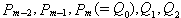 五点共面; 五点共面;
��Pm-2和Q2或者同在直线
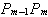 上或者位于直线 上或者位于直线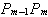 的同侧,并且
的同侧,并且
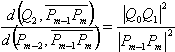 , , |
其中,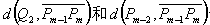 分别表示点Q2和Pm-2到直线
分别表示点Q2和Pm-2到直线
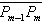 的距离。 的距离。
|