从图5.8容易得到斜投影变换的公式为:
tgα=z/L 。 令L1=L/z,则上式改写为:
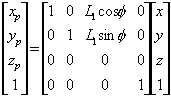
在PHIGS图形标准中,设投影向量在观察坐标系中的坐标为:p(px ,py ,pz), 则其一般性的投影变换矩阵为: 通常选φ=30o或45o,这将显示物体的前面、侧面和顶面(或底面)。在斜平行投影中,若适当选取α的值,使得tanα=1或者tanα=2(即:α=45o或者α≈63.4o),则分别得到斜等侧投影和斜二侧投影。 |
从图5.8容易得到斜投影变换的公式为:
tgα=z/L 。 令L1=L/z,则上式改写为:
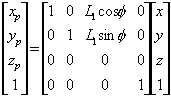
在PHIGS图形标准中,设投影向量在观察坐标系中的坐标为:p(px ,py ,pz), 则其一般性的投影变换矩阵为: 通常选φ=30o或45o,这将显示物体的前面、侧面和顶面(或底面)。在斜平行投影中,若适当选取α的值,使得tanα=1或者tanα=2(即:α=45o或者α≈63.4o),则分别得到斜等侧投影和斜二侧投影。 |