|
二、一般旋转
绕坐标原点的任意旋转都可以看成是相继绕三个坐标轴旋转的结果。虽然旋转的顺序可以不唯一,但是结果却是一样的。假如我们将物体绕x轴旋转α角度,其旋转矩阵为
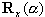 ,再绕y轴旋转β角度,其旋转矩阵为 ,再绕y轴旋转β角度,其旋转矩阵为
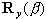 ,最后再绕z轴旋转γ角度,其旋转矩阵为 ,最后再绕z轴旋转γ角度,其旋转矩阵为
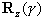 ,则其组合变换矩阵为 ,则其组合变换矩阵为
R =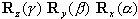 。
。
现在,请思考:相对于空间任意点,绕x, y和z轴分别旋转α,β和γ角度,其旋转变换的组合变换矩阵如何求?
三、绕任意轴的旋转
假定我们已知一个立方体,见图4.9 (a),它绕固定点P 0且由矢量P1-P0所指定的方向轴旋转θ角度(规定:面向旋转轴的正向观察,逆时针的转角为正,(左图4.9)
θ>0;否则θ<0),如何求它的变换矩阵呢?
首先,作平移变换T(-P0),使参考点P0点与坐标原点重合(如图4.9 (b)所示);然后,求绕矢量u=P1-P0旋转θ角的旋转变换矩阵R(θ);最后作平移变换T(P0),恢复原来的坐标系。
求R(θ)的方法很多。例如:我们可以通过坐标系的一系列的旋转变换使u与坐标系的z轴重合后,再绕z轴旋转θ角度,最后再作相应的坐标系的一系列逆旋转变换,从而得到变换矩阵R(θ);我们也可以通过改变坐标系框架和旋转变换得到R(θ)。对于前者,大家可以自己练习。下面,我们介绍后一种方法。
��令坐标系oxyz的坐标系框架用(e1,
e2, e3, o)表示,新坐标系P0XYZ的坐标系框架用(i, j,
k, P0)表示,并且两个坐标系的原点重合,即o=P0,见图4.9 (b),我们可以通过改变坐标系框架来实现坐标变换:
在坐标系P0XYZ中,P0Z轴与u=P1-P0重合,其单位矢量
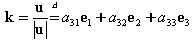 , ,
P0X轴可取在经过P0点并与P0Z轴垂直的任一直线上。
|