图4.10 u在xoy平面上的投影

如果

，则P₀X轴方向的单位矢量为

；
如果

=0，则取

。
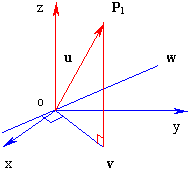
P₀Y轴方向的单位矢量为

，即

。
坐标系P₀XYZ的原点

。
上述等式可以用矩阵表示为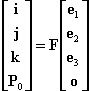

（4－3－8）

其中，F是4×4矩阵，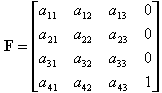

（4－3－3）式称为坐标系框架变换的矩阵表示。
假定P是在坐标系oxyz（其坐标系框架用（e₁, e₂, e₃, o）表示）中的一个点（或矢量）的齐次坐标表示，它在坐标系P₀XYZ（其坐标系框架用（i, j, k, P₀）表示）中的齐次坐标用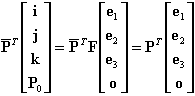

表示，则有

（4－3－9）

，
所以，从坐标系P₀XYZ到坐标系oxyz的坐标变换为

（4－3－10）

。
由于i, j和k是互相正交的单位矢量，显然，当

时，矩阵F的行向量也是互相正交的单位向量，所以F是一个正交矩阵，即

。于是，从坐标系oxyz到坐标系P₀XYZ的坐标变换为

（4－3－11）

。
根据4.3.2节讲的绕坐标轴作旋转变换的方法，利用（4－3－2）、（4－3－4）和（4－3－5）式，可以得到变换公式为

（4－3－12）

。
这个变换过程可以理解成为：先从坐标系oxyz变换到坐标系P₀XYZ，紧接着绕P₀Z轴旋转θ角，再作坐标系的逆变换：从坐标系P₀XYZ变换到坐标系oxyz，使坐标系复原。
最后，我们得到总的组合变换矩阵为：

（4－3－13）