现在,我们可以通过以下三步来实现相对于Pc点的比例变换(见图4.8): 1) 将长方体平移到坐标原点: P′ = T(-Pc)P; 2) 对长方体作比例变换:P′′=S( 3) 作第一步变换的反变换,恢复原先的坐标系:P′′′ = T(Pc)P′′。即 P′′′ = M P, 其中,M 称为相对于Pc点的比例变换矩阵,即组合变换矩阵。 M = T(Pc) S( 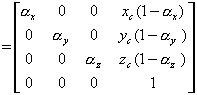 。
。
|
现在,我们可以通过以下三步来实现相对于Pc点的比例变换(见图4.8): 1) 将长方体平移到坐标原点: P′ = T(-Pc)P; 2) 对长方体作比例变换:P′′=S( 3) 作第一步变换的反变换,恢复原先的坐标系:P′′′ = T(Pc)P′′。即 P′′′ = M P, 其中,M 称为相对于Pc点的比例变换矩阵,即组合变换矩阵。 M = T(Pc) S( 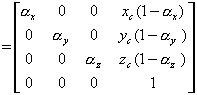 。
。
|