1. 在齐次坐标系中,写出下列变换矩阵:
(a) 整个图象放大2倍;
��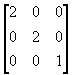
(b) y向放大4倍和x向放大3倍;
��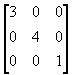
(c) 图象上移10个单位和右移5个单位;
��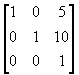
(d) 保持x=5和y=10 图形点固定,图象y向放大2倍和x向放大3倍;
(1) 将坐标系平移到点(5,10)
T1 = 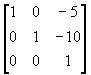
(2) 将图象y向放大2倍和x向放大3倍
S = 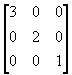
(3) 平移坐标系至(-5,-10)点
T2 = 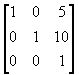
T = T2 ・S・T1 =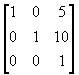
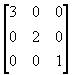
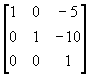 =
=
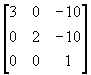
(e) 图象绕坐标原点顺时针方向转π/2;
R = 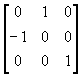
(f) 图象绕点x=2和y=5反时针方向转π/4。
(1) 将坐标系平移到点(2,5);
T1 = 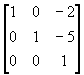
(2) 将图象绕原点反时针方向转π/4;
R = 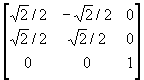
(3) 将坐标系平移到点(-2,-5);
T2 = 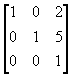
T = T2 ・R・T1 = 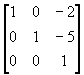
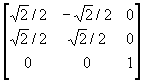
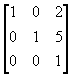
= 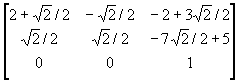
2. 由比例、平移和旋转变换构成的复合变换,仅在某些情况下交换次序不影响总的变换效果,它们是哪几种两个变换的组合。
��(1) 两个连续的平移变换;
��(2) 两个连续的比例变换;
��(3) 两个连续的旋转变换;
��(4) 比例系数相等的比例变换和旋转变换。
3. 写出由部分图形产生满足下列条件的另一部分图形的变换矩阵:
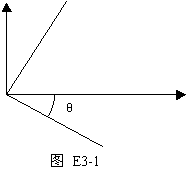
(a) 对y轴对称;
��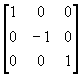
(b) 对x轴对称;
��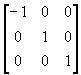
(c) 对坐标原点对称;
��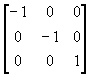
(d) 对直线y=x成轴对称;
��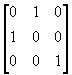
(e) 对直线y=-x成轴对称;
��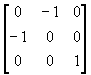
(f) 对图E3所示方向进行比例系数为S1 和S2的图形;
(1) 将图形绕原点逆时针方向旋转θ角;
R1 = 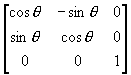
(2) 在x方向上的比例系数为S1,y方向的比例系数为S2;
S = 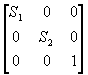
(3) 将图形绕原点顺时针方向旋转θ角。
R2 = 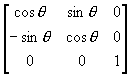
M = R2 R1 = 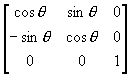
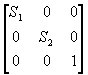
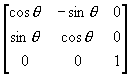
= 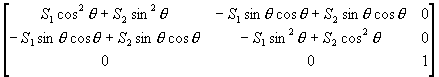
(a) 对直线y=mx+b对称的图形。
(1) 当m = 0时;
T1 =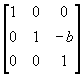 T2 =
T2 = 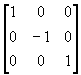 T3
=
T3
= 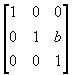
M = T3T2T1 = 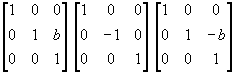 =
=
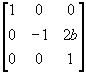
(2) 当m ≠ 0,b = 0时,以第一象限为例;
T1 =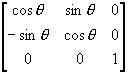 T2 =
T2 = 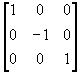 T3
=
T3
= 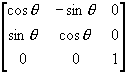
M = T3 T2 T1 = 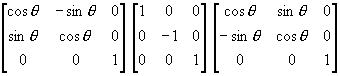
= 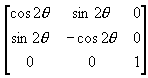
因为,tanθ = m,cos2θ = (1-m2) �M (1+m2),sin2θ = 2m / (1+m2)
(3) 当m ≠ 0,b ≠ 0时,以第一象限为例。
T1 =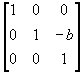 T2 =
T2 =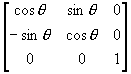 T3 =
T3 = 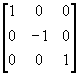
T4 =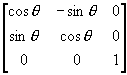 T5 =
T5 = 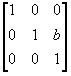
M = T5T4T3T2T1
= 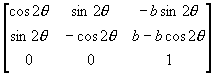
4. 对直线L: ax+by+c=0,用齐次坐标方式可以写出矩阵乘法形式p・l=0,即
��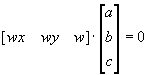
(a) 证明空间一点![]() 与直线L的距离等于
与直线L的距离等于 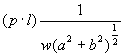
(b) 求出与直线平行且经过点(x1,y1)的另一直线方程系数a`、b`和c`和系数a、b和c的关系式;
��a` = a; b`= b; c`= -a x1- by1
(c) 求出与直线垂直并且经过点(x2,y2)的另一直线方程系数a`、b`和c`和系数a、b和c的关系式
��a` = -b; b`= a; c`= -b x2- ay2;
5. 程序中用Set-Window(xmin ,xmax
,ymin ,ymax)和Set-Viewport(xmin ,xmax,ymin
,ymax) 来设定二维视见变换。
(a) Set-Window(10,100,10,150)和 Set-Viewport(0,0.25,0,0.25) ,则在齐次坐标系中的视见变换矩阵是什么?
��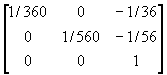
(b) 显示与(a)同样的图形,但显示图形在x向为(a)的1.5倍,y向为(a)的2倍,且视见区右下角位置不变。请写出Set-Window和Set-Viewport中的参数值;
(c) 从(a)中显示图形中选出右一半图形使它放大显示在(a)中规定的视见区上,请写出Set-Window和Set-Viewport中的参数值。
6. 若已知某一正方形显示器的坐标范围是以dxmin ,dxmax ,dymin
和dymax规定的矩形区,且(dymax - dymin ) = 3/4
* (dxmax - dxmin),为保证图形不失真并充分利用显示区,请写出自用户坐标至该显示器坐标的视见变换阵。
7. 若窗口函数在定义为平行于用户坐标轴的直立矩形后,还允许此窗口再绕左下角旋转θ角,写出由旋转后窗口到直立矩形视见区的变换矩阵。
假设窗口左下角坐标为(xw1,yw1),右上角坐标为(xw2,yw2)
(1) 平移直立矩形视见区的左下角顶点到坐标原点;
��T1 =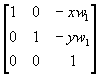
(2) 将此窗口再绕左下角逆时针旋转θ角。
R = 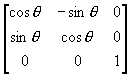
M-1 = RT1
M = 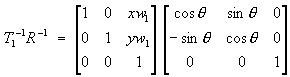
= 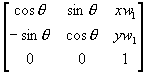
8. 二维图形绕原点的旋转公式是x`=x cosθ - y sinθ和y`=x sinθ + y cosθ。为快速产生连续旋转图形,考虑到每次旋转θ(弧度)很小,因此可用公式x`=x
- y θ和y`=x θ + y 来代替,或用x`=x - y sinθ和y`=x`sinθ + y 来更好地代替。用程序实现精确和近似计算的图形旋转,并比较之。注意,近似计算将引入误差。按每次旋转角的大小,可在总旋转角达π/2,
π,3π/2和π等一些特殊位置上用精确计算。
9.下面是依次序给出的多边形顶点坐标,请指出哪些是凸多边形?你是如何判断的?
��对凸多边形求出向内法矢量。
��(a) (2,3),(7,2),(10,6),(8,11),(3,8);
����凸多边形;内法向量依次为(-1,-5), (4,-3), (5,2), (-3,5), (-5,1)
��(b) (1,4),(4,1),(8,3),(8,8),(5,5);
��(c) (4,4),(5,1),(7,4),(5,8),(2,4);
��(d) (3,8),(7,10),(8,6),(9,2),(3,2)。
��(b) (c) (d) 均不是凸多边形。
10.对上题中的一个凸多边形求出下列线段经剪取后的端点坐标。
��(a) p1 =(3,4),p2 =(7,7);
��在凸多边形内
��(b) p1 =(1,4),p2 =(3,14);
��在凸多边形外
��(c) p1 =(1,12),p2 =(8,12);
��在凸多边形外
��(d) p1 =(13,1),p2 =(6,5)。
��(8.275,3.7) 和 (6,5)
11.对旋转的直立矩形窗可以用Cyrus-Beck算法进行剪取,也可对图形先进行变换,使剪取窗成直立矩形再采用Sutherland-Cohen算法进行剪取,比较这两种方法,哪一种计算量少。在你的图形系统上实现Cyrus-Beck算法,并对一组线段进行剪取验证你前面的结论。
12 用矩形窗剪取具有N个顶点的凸多边形,剪取后的多边形最多有多少顶点?最少有多少顶点?若对凹多边形剪取,并只产生一个剪取后多边形,那么最多有多少顶点?
��(1) N + 4个顶点
��(2) 最少3个顶点
��(3) ???
13 试说明为什么Sutherland-Hodgmen算法只能用于凸的剪取区域?如何去除该算法产生的多余的边?
14 为何任意形状多边形之间进行剪取的Weiler-Atherton算法规定多边形内外边界顶点要采用不同的次序排列,主多边形和剪取多边形的外边界或内边界采取相同的次序排列?
15 写出在任意形状多边形之间进行剪取的Weiler-Atherton算法的伪码表示,在你的图形系统中实现Weiler-Atherton算法。并对各种形状和相互关系的剪取多边形和主多边形进行剪取操作以检查程序的完整性和正确性。
16 写出实现凸多边形剪取体对多边形进行剪取的一种算法的详细步骤。
17 写一个程序实现任意多边形之间剪取的Weiler-Atherton算法,对主多边形外边顶点是(0,0),(20,0),(20,-20),(0,-20)内部孔边界顶点是(7,-13),(13,-13),(13,-7),(7,-7)
和窗多边形的外部边界是(-10,-10),(-10,10),(10,10),(10,-10)和内部孔是(-5,-5)(5,2.5),(5,5),(2.5,5)进行剪取。求出进入与离开的交点,写出剪取后多边形顶点表。