|
即
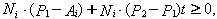
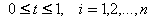 。
。
令D=P2-P1。如果Ni・D=0,则表明:或者P1=P2,即线段P1P2是一个点;或者线段P1P2与边界Ei平行(一般视为无交点,可以忽略)。
如果P1=P2,那麽:
当 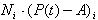 >0时,点P1位于裁剪区域内部;
>0时,点P1位于裁剪区域内部;
当 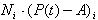 =0时,点P1位于裁剪边界上; =0时,点P1位于裁剪边界上;
当 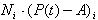 <0时,点P1位于裁剪区域外部。 <0时,点P1位于裁剪区域外部。
如果Ni・D≠0,可以从上式得到线段P1P2与裁剪边界Ei的交点参数:
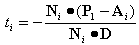 。 。
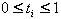 时,表明线段P1P2与裁剪边界Ei或Ei的延长线有交点;否则它们没有交点,可以忽略。虽然线段与凸多边形至多有2个交点,但是满足 时,表明线段P1P2与裁剪边界Ei或Ei的延长线有交点;否则它们没有交点,可以忽略。虽然线段与凸多边形至多有2个交点,但是满足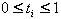 (
( 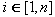 )的交点可能有多个,每个交点对应于凸多边形的一条边界。 )的交点可能有多个,每个交点对应于凸多边形的一条边界。
��当Ni・D>0时,如果我们沿线段L1的端点P1向P2移动,就会跨越裁剪边界Ei而进入该边界的内侧半平面,其交点用PE表示(见图3.13,其交点参数值为t1。请在图中用动画表示出来。),它靠近线段的起点;这样的交点参数值的集合可以表示为PE(ti)={
ti | Ni・D>0,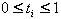 }。反之,Ni・D<0时,如果我们沿线段L1的端点P1向P2移动,就会跨越裁剪边界Ei而离开该边界的内侧半平面,其交点用PL表示(见图3.12,其交点参数值为t5。请在图中用动画表示出来。),它靠近线段的终点;我们把这样的交点参数值的集合表示为PL(ti)={
ti | Ni・D<0,
}。反之,Ni・D<0时,如果我们沿线段L1的端点P1向P2移动,就会跨越裁剪边界Ei而离开该边界的内侧半平面,其交点用PL表示(见图3.12,其交点参数值为t5。请在图中用动画表示出来。),它靠近线段的终点;我们把这样的交点参数值的集合表示为PL(ti)={
ti | Ni・D<0,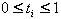 }。我们只要从PE(ti)中选出最大值
}。我们只要从PE(ti)中选出最大值 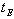 ,从PL(ti)中选取最小值 ,从PL(ti)中选取最小值
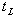 ,由参数范围( ,由参数范围(
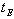 , ,
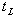 )所定义的线段就是裁剪后的结果。 )所定义的线段就是裁剪后的结果。
考虑到参数的有效范围 ,我们有
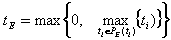 , ,
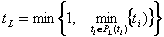 。 。
如果tE>tL,如图3.12中的线段L2所示,则表明线段P1P2位于裁剪区域以外,整条线段都应当舍弃。
当凸多边形为矩形且矩形的边平行于坐标轴时,上述算法可简化为Liang-Barsky算法。
|