计算机图形学

Liang-Barsky算法步骤：
1) 令u₁=0.0，u₂=1.0，k=1；
2) 按参数化形式写出裁剪条件：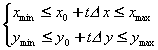

这4个表达式可以统一表示为：

；
其中，
　　p₁ = -Δx, q₁ = x₀ - x_min;
　　p₂ = Δx, q₂ = x_max - x_0;
　　p₃ = -Δy, q₃ = y₀ - y_min;
　　p₄ = Δy, q₄ = y_max - y_0。
3) 如果p_k≠0：
　　a) 如果p_k<0，u₁ = max{ u₁,r_k=q_k/p_k };
　　b) 如果p_k>0，u₂ = min{ u₂,r_k=q_k/p_k };
　　c) 如果u₁>u₂，则线段位于裁剪区域之外，舍弃之，转8)；否则，转5）；
4) 如果p_k=0，则表示直线平行于第k条裁剪边界（k=1,2,3,4分别对应于左、右、下、上边界）。
　　a) 如果同时还满足q_k<0，则该线段完全在裁剪边界外，舍弃之，转8)；否则，转5）；
5) k++;
6) 如果k≤4，转3）；否则，转7）；
7) t∈[u₁,u₂]的线段就是原线段P₀P₁的可见部分，应当保存或显示；
8) 结束。