|
��光栅图形显示器可以看成是由许多可发光的离散点(即像素)组成的矩阵,它需要专门的算法来生成直线、圆弧和曲线等等图形。本章将介绍生成光栅图形的相关算法。这些算法对于开发图形设备驱动程序是必需的。不过,在Windows、Unix或Linux操作系统上开发计算机图形时,现在都有支持OpenGL的图形硬件和软件开发工具可供使用,而OpenGL程序库本身都提供了光栅图形显示的驱动程序,这为图形软件开发人员提供了便利。
2.1画线算法
��在数学上,理想的点和直线都是没有宽度的。但是,由于每个像素对应于图形设备上的一个矩形区域,当我们在光栅图形设备上显示一个点时,实际上它是有用一个发光的矩形区域来表示的;当在光栅图形设备上显示一条直线时,我们只能在显示器所给定的有限个像素组成的矩阵中,按扫描线顺序,依次确定最佳逼近于该直线的一组像素,并且对这些像素进行写操作。这个过程称为直线的扫描转换。
��对于水平线、垂直线和45º斜线,选择哪些像素是显而易见的,但是对于其它的直线,确定用哪些像素来表示它就不那麽简单了。本节我们介绍用于直线扫描转换的常用算法:Bresenham画线算法。
��在介绍画线算法之前,我们先讨论画直线的基本要求:直线必须有精确的起点和终点,外观要直,线宽应当均匀一致、且与直线的长度和方向无关,最后,算法速度要快。
��Bresenham算法是计算机图形学领域使用最广泛的直线扫描转换算法。该方法最初是为数字绘图仪设计的,后来被广泛地应用于光栅图形显示和数控(NC)加工。该算法构思巧妙,使得每次只需检测误差项的符号就能决定直线上的下一个像素的位置。算法原理如下:过各个像素的中心构造一组虚拟网格线,首先按直线从起点到终点的顺序计算直线与各垂直网格线的交点,然后,采用增量计算,使得对于每一列,只要检查一个误差项的符号,就可以确定该列像素中与此交点最近的像素。
��先考虑斜率k=dy/dx≤1的直线。如图2.1所示,设直线 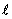 方程为
方程为 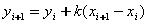 ,其中,k = dy/dx。 假设当前像素的x坐标已经确定为xi,其y坐标为yi,由于坐标(xi,yi)(i=0,1,…)只能取整数,那么下一个像素的x坐标 ,其中,k = dy/dx。 假设当前像素的x坐标已经确定为xi,其y坐标为yi,由于坐标(xi,yi)(i=0,1,…)只能取整数,那么下一个像素的x坐标 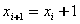 ,而yi+1的坐标有两种可能:
,而yi+1的坐标有两种可能:
��1)
保持不变,即y
i+1=yi;或者
��2)
y坐标递增1,即y i+1=yi+1。
��令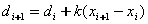 ,y坐标是否增加1取决于如图所示误差项d i的值。因为直线的起始点在像素中心,所以初始误差d0=0。x每增加1,y的值相应递增直线的斜率值k,即
,y坐标是否增加1取决于如图所示误差项d i的值。因为直线的起始点在像素中心,所以初始误差d0=0。x每增加1,y的值相应递增直线的斜率值k,即 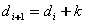 。一旦di+1≥1,就把它减去1,这样保证di+1在0~1之间。当d i+1≥0.5时,直线
。一旦di+1≥1,就把它减去1,这样保证di+1在0~1之间。当d i+1≥0.5时,直线 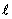 与x=xi+1的垂线的交点最接近于当前像素(xi,yi)的右上方像素(xi+1,yi+1);而当d i+1<0.5时,其交点更接近于(xi,yi)右边的像素(xi+1,yi)。为方便计算,令e0=-0.5,e i+1=di+1-0.5,增量为k。当ei+1≥0时,取当前像素(xi,yi)的右上方像素(xi+1, yi+1);而当e i+1<0时,更接近于右方像素(xi+1,yi)。
与x=xi+1的垂线的交点最接近于当前像素(xi,yi)的右上方像素(xi+1,yi+1);而当d i+1<0.5时,其交点更接近于(xi,yi)右边的像素(xi+1,yi)。为方便计算,令e0=-0.5,e i+1=di+1-0.5,增量为k。当ei+1≥0时,取当前像素(xi,yi)的右上方像素(xi+1, yi+1);而当e i+1<0时,更接近于右方像素(xi+1,yi)。
|