|
这里给出Cannon矩阵乘法例子。计算任务描述如下:
A,B为n×n维的稠密矩阵。计算A,B的积,并存放到C,即:
C = A × B
Cannon的矩阵乘法算法把p个处理器看成是一个二维的网格,各处理器在网格的坐标记为p(i, j),其中i,j = 0, 1,
...,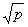 -1。并将A,B,C分别划分为 -1。并将A,B,C分别划分为 的块,对各块编号,将A(i,j),B(i,j),C(i,j)分给p(i,j)。当完成数据初始赋值后,Cannon的算法按步进行,在每一步中,每个处理器完成本地的A(i,j)和B(i,j)(它们都是 的块,对各块编号,将A(i,j),B(i,j),C(i,j)分给p(i,j)。当完成数据初始赋值后,Cannon的算法按步进行,在每一步中,每个处理器完成本地的A(i,j)和B(i,j)(它们都是 的矩阵)的乘法,然后将A发送给自己左边的处理器,B发送给自己上边的处理器(边界上的处理器回绕)。算法完成后,C的值按块分布在各个处理器上。 的矩阵)的乘法,然后将A发送给自己左边的处理器,B发送给自己上边的处理器(边界上的处理器回绕)。算法完成后,C的值按块分布在各个处理器上。
//Canno's MM algorithm.
#include <stdlib.h>
#include <mpi.h>
//将处理器的网格坐标转换为处理器号
int CartToRank(int row, int col, int npdim)
{
return ((row+npdim)%npdim)*npdim + (col+npdim)%npdim;
}
//块矩阵相乘
void MatrixMultiply(int nlocal, double *a, double *b, double *c)
{
int i,j,k;
for( i = 0; i < nlocal; i++ )
for( j = 0; j < nlocal; j++ )
for( k =0; k < nlocal; k++ )
{
c[i,j] += a[i,k] * b[k,j];
}
}
void main(int argc, char **argv)
{
int i;
int n, nlocal;
double *a, *b, *c, *wspace;
int npes, npdim;
int myrank, myrow, mycol;
MPI_Status status;
/* 初始化,得到系统信息 */
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &npes);
MPI_Comm_rank(MPI_COMM_WORLD, &myrank);
if (argc != 2) {
//需要给出矩阵的维数
if (myrank == 0)
printf("Usage: %s <the dimension of the matrix>\n",
argv[0]);
MPI_Finalize();
exit(0);
}
//矩阵的维数
n = atoi(argv[1]);
//处理器网格每一维的处理器数
npdim = sqrt(npes);
if (npdim*npdim != npes) {
//处理器数目必须是平方数
if (myrank == 0)
printf("The number of processes must be a perfect square.\n");
MPI_Finalize();
exit(0);
}
//本地的块矩阵的维数
nlocal = n/npdim;
//根据处理器号得到自己在处理器网格的坐标(myrow, mycol)
myrow = myrank/npdim;
mycol = myrank%npdim;
//分配本地计算所需的空间
a = (double *)malloc(nlocal*nlocal*sizeof(double));
b = (double *)malloc(nlocal*nlocal*sizeof(double));
c = (double *)malloc(nlocal*nlocal*sizeof(double));
wspace = (double *)malloc(nlocal*nlocal*sizeof(double));
//给矩阵赋初值(a,b的内容实际上没有实际意义)。
srand48((long)myrank);
for (i=0; i<nlocal*nlocal; i++) {
a[i] = b[i] = drand48();
c[i] = 0.0;
}
/* Perform the initial matrix alignment. First for a and then
for b */
/* 进行初始对齐,先a再b。设处理器坐标为(i,j),则本地的a将传给 p(i, j-i),
即左移i列,b将传给p(i-j,j),即上移j列*/
/* MPI_Sendrecv的形式
int MPI_Sendrecv(void *sendbuf, int sendcount, MPI_Datatype senddatatype,
int dest, int sendtag, void *recvbuf, int recvcount,
MPI_Datatype recvdatatype, int source, int recvtag,
MPI_Comm comm, MPI_Status *status)
*/
MPI_Sendrecv(a, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol-myrow, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol+myrow, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(a, wspace, nlocal*nlocal*sizeof(double));
MPI_Sendrecv(b, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow-mycol, mycol, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow+mycol, mycol, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(b, wspace, nlocal*nlocal*sizeof(double));
/* 主循环*/
for (i=0; i<npdim; i++) {
MatrixMultiply(nlocal, a, b, c); /* c = c + a*b */
/* a左移 */
MPI_Sendrecv(a, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol-1, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol+1, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(a, wspace, nlocal*nlocal*sizeof(double));
/* b 上移1 */
MPI_Sendrecv(b, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow-1, mycol, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow+1, mycol, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(b, wspace, nlocal*nlocal*sizeof(double));
}
/*得到原来的a,b,不是必须,但可以检验算法实现 */
MPI_Sendrecv(a, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol+myrow, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow, mycol-myrow, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(a, wspace, nlocal*nlocal*sizeof(double));
MPI_Sendrecv(b, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow+mycol, mycol, npdim),
1, wspace, nlocal*nlocal, MPI_DOUBLE,
CartToRank(myrow-mycol, mycol, npdim),
1, MPI_COMM_WORLD, &status);
memcpy(b, wspace, nlocal*nlocal*sizeof(double));
//算法完成
if (myrank == 0)
printf("Done multiplying the matrices!\n");
free(a);
free(b);
free(c);
free(wspace);
MPI_Finalize();
}
|